不同的坐标表示及转换
- 此处的大地坐标系与上文不同,上文所指与天文坐标系相对(一簇)
- 大地地理坐标又称大地坐标,表示地面点在参考椭球面上的位置
- 基准是参考椭球面和法线,用大地经度 L 和大地纬度 B 表示
- P 点大地经度 L:过 P 点的大地子午面和首子午面所夹的两面角
- P 点大地纬度 B:过 P 点的法线与赤道面的夹角
- P 点大地高 H :P 点沿法线到参考椭球面的距离(注意与海拔的区别)
空间直角坐标系:
- 坐标原点 O:地球椭球体中心(与质心重合)
- Z 轴方向: 指向地球北极
- X 轴方向: 指向格林尼治子午面与地球赤道面之交点
- Y 轴方向: 垂直于 XOZ 平面,构成右手坐标系。
空间直角坐标与大地坐标间的转换:
卯酉圈:纬圈,N 为卯酉圈的偏心率
左右都有 B,需要迭代求解——达到一定精度停止
平面直角坐标系:
大地坐标计算复杂,小范围内使用不够方便——所以局部地区测量最好用平面直角坐标系。
我国采用的高斯-克吕格正形投影(简称高斯投影)
变形
(B,L)——>(x,y)
即$x=f_x(B. L)$,$y=f_y(B, L)$
需要设定一定的边界条件——中央子午线不变、保角?
高斯投影属于保角投影——地球上方位与地图上方位保持不变,球面上的角度投影到横椭圆柱面上后保持不变,而距离将变长
分带投影——带宽问题——变形与误差——分带越多——效率越低
最好分为 6°带
因此带号 N 与中央子午线经度$L_0$的关系:$L_0=6N-3$,$N=INT(L/6)+1$
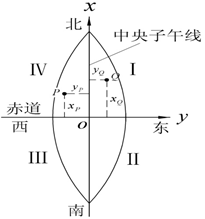
x轴与y轴互换了位置
象限按顺时针方向编号,以保证各类三角函数计算可直接在高斯平面直角坐标系中进行
把中央子午线移动 500km
为确定投影带的位置,还在y坐标前冠以带号
例:xm=1346216.985m ym=19634527.165m 19 为带号数
真实坐标(1346216.985, 134527.165)
如果选用 3°带
三度带奇数中央子午线与六度带重合
因此带号 N 与中央子午线经度$L_0$的关系:$L_0=3N$,$N=INT((L-1.5)/3)+1$
我国大陆所处的经度范围是东经 73°27′~东经 135°09′
统一 6°带投影与统一 3°带投影的带号范围分别为 13~23,25~45
两种投影带的带号不重复,根据y坐标前的带号可以判断属于何种投影带
独立坐标系:
- 原点、坐标轴、坐标轴的尺度
- 为什么?——国家安全、减小投影变形、使用方便
- 保密作用——把中央子午线定在城市中心位置——形成独立坐标系——抬高投影面——平均海拔较高——地球、参考椭球——计算出的长度基本一致等等
- 例如长江大桥建桥——桥轴线为 x 轴
- 地面点的高程系统
- 绝对高程:地面点沿铅垂线到大地水准面的距离,也称海拔,简称高程
- 相对高程:地面上一点到假定水准面的铅垂距离(H′)
- 高 差:地面上两点间的高程之差(h)
- 在海边设立验潮站(tide gauge station),进行长期观测,求得海水面的平均高度作为高程零点,以通过该点的大地水准面为高程基准面(height datum)。建在海边——测量海面高度的站——验潮站——测量水准点与
- 大地水准面上的高程恒为零
- 我国有两个国家高程系统:(1)1956 年黄海高程系(2)“1985 国家高程基准”
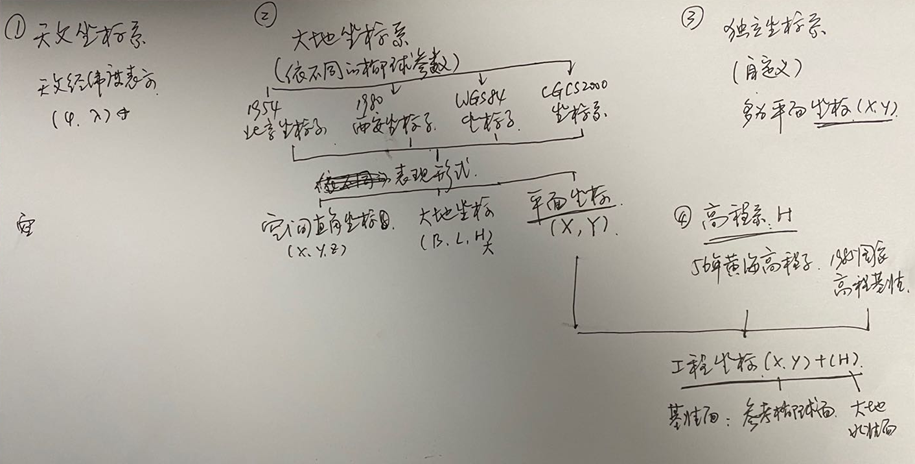
确定地面点的坐标
地面点的坐标表示
坐标系:54 坐标系/80 坐标系/CGCS2000/WGS84
可以直接采用三维坐标表示(空间直角坐标、大地坐标)
- 空间直角坐标(XYZ,简单但不直观)
- 大地坐标(BLH,直观但不方便,大地高不能在工程中直接应用)
- 是采用空间定位技术(如卫星定位)时最常用的点的表示方法
平面和高程分别表示(2+1 维)
- 平面坐标:xy 高斯投影或独立坐标
- 高程:h 海拔高程
- 简单、直观,方便工程应用
- 缺点:平面与高程分离,不是真三维坐标,不利于空间定位技术(如卫星定位)的发展
- 是我国目前最常用的地面点的表示方法
确定地面某点的平面坐标
- 首先需要确定坐标系,常采用平面直角坐标
- 国家坐标系(高斯平面直角坐标)
- 独立坐标系(通常以西南角为原点,X 指北,Y 指东)
- 需要足够的起算数据(没有时可假定)
- 需要采用一定的测量方法
- 需要有足够的观测量
- 首先需要确定坐标系,常采用平面直角坐标
确定地面某点高程
常规测量的基本工作
- 测距离 D
- 测角度β
- 测高差 h
确定地面点坐标的基本概念
- 地球表面的形状
- 地貌:地球表面高低起伏的形态,例如:高山、峡谷等
- 地物:地面上人造或天然固定物体,例如:建筑、桥梁、道路等
- 测量的主要任务是测定和测设,变形监测
测定——将地物和地貌按一定的比例尺缩小绘制成地形图
测设——将设计图纸上的点放到实地上
变形监测——需要看各类物的变形
- 碎部测量与控制测量
- 地物、地貌的特征点又称碎部点,测量碎部点坐标的方法与过程称为碎部测量
- 例如测量房子就叫碎步测量
- 在测量碎部点坐标之前需要布设一些已知点,测量上将这些已知点称为控制点,测量与计算控制点坐标的方法与过程称为控制测量
方位角
- 由直线一端–标准方向的北端起,顺时针量至某一直线的水平夹角,称为该直线的方位角,其取值范围是 0°~360°
- 标准方向:
- 真北方向:过真子午线上任一点所作的切线方向。采用天文测量的方法测定,如观测太阳、北极星等,也可用陀螺经纬仪测定。在北半球,不同点处的真北方向收敛于地球的北极。(方位角称为真方位角用$A$表示)
- 磁北方向:过磁子午线上任一点所作的切线方向。可用指南针测定。磁针自由静止时,其北端所指方向即为磁北方向。在北半球,不同点处的磁北方向收敛地球的磁北极(称为磁方位角用$A_m$表示)
- 坐标北方向:坐标纵轴(x 轴)正向所示方向,称为坐标北方向。在同一坐标系中,各点处的坐标北方向是相互平行的。
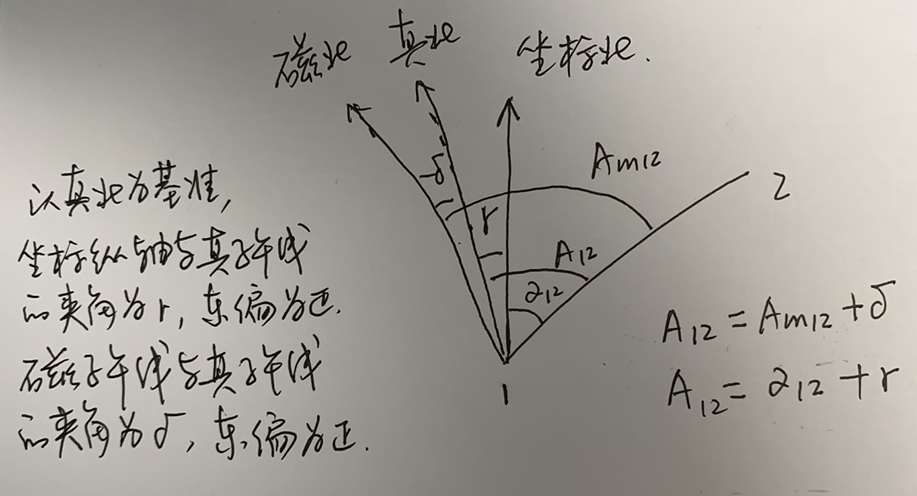
- 坐标北方位角——本学期主要
方位角的计算:
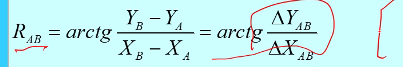
- 注意值域的映射——方位角的关系
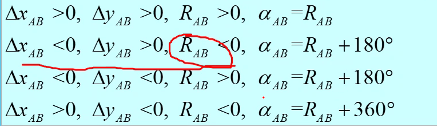
由于地面两点真(磁)子午线不平行,存在子午线收敛角和磁偏角,则真(磁)方位角的正、反方位角不是差 180°只有坐标方位角才满足上式关系。
坐标方位角的确定:通过已知坐标反算;通过与已知边的连测推算
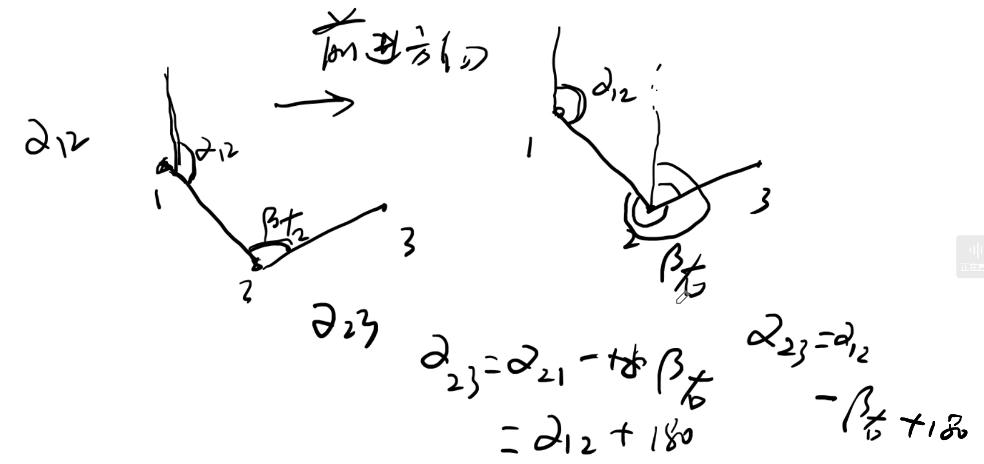
- 非常
重要 - 坐标正算
- 已知:
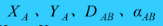
- 求:

- 坐标反算
- 已知:
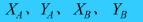
- 求:

常用方法
- 极坐标法,已知两点坐标,求另一点坐标
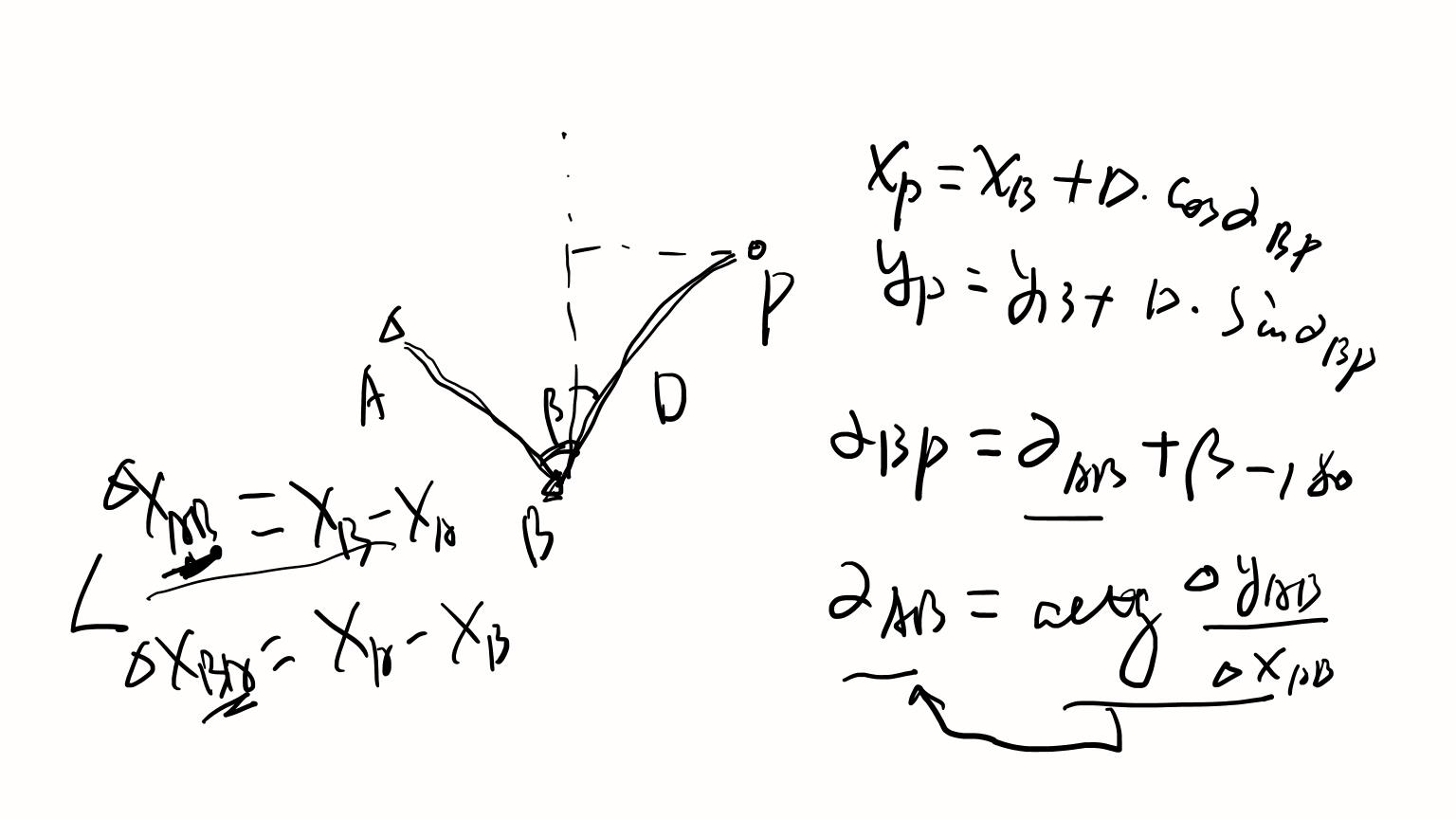
- 前方交会
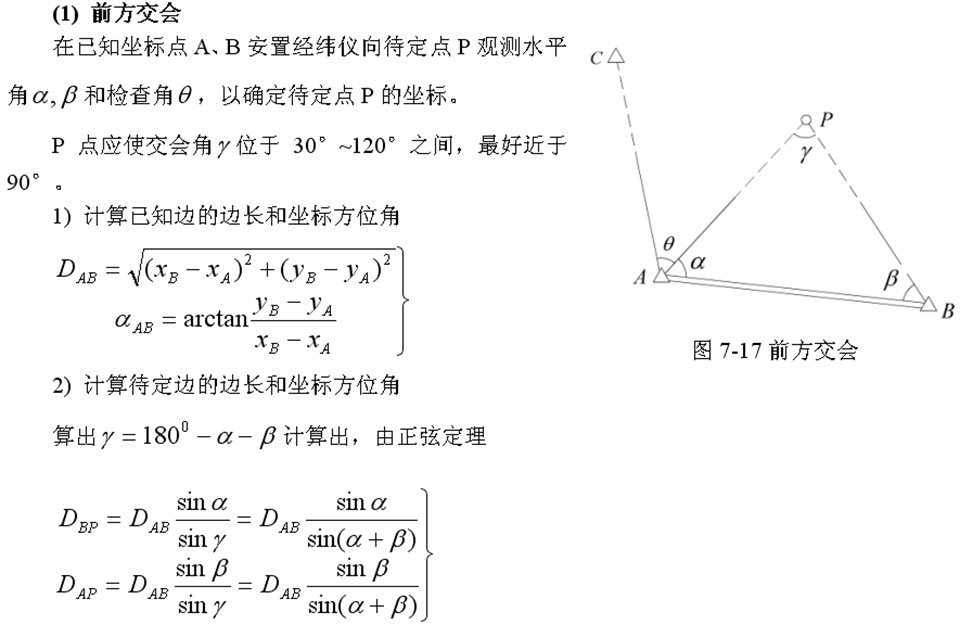
- 后方交会
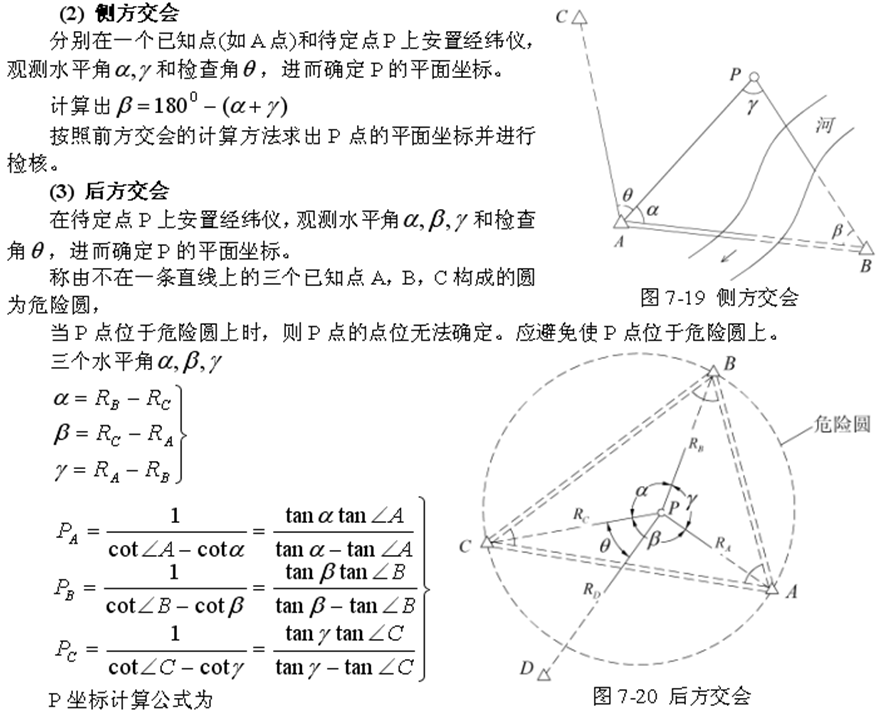
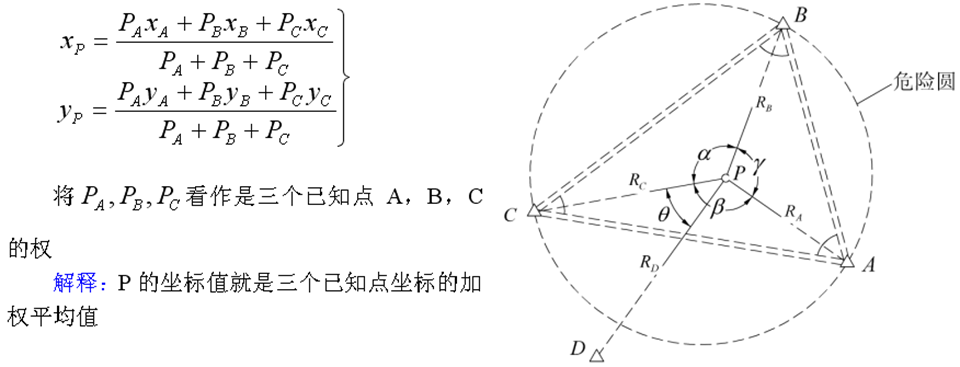
- 注意:前方交会顺序必须是顺时针!逆时针需要将角度反号
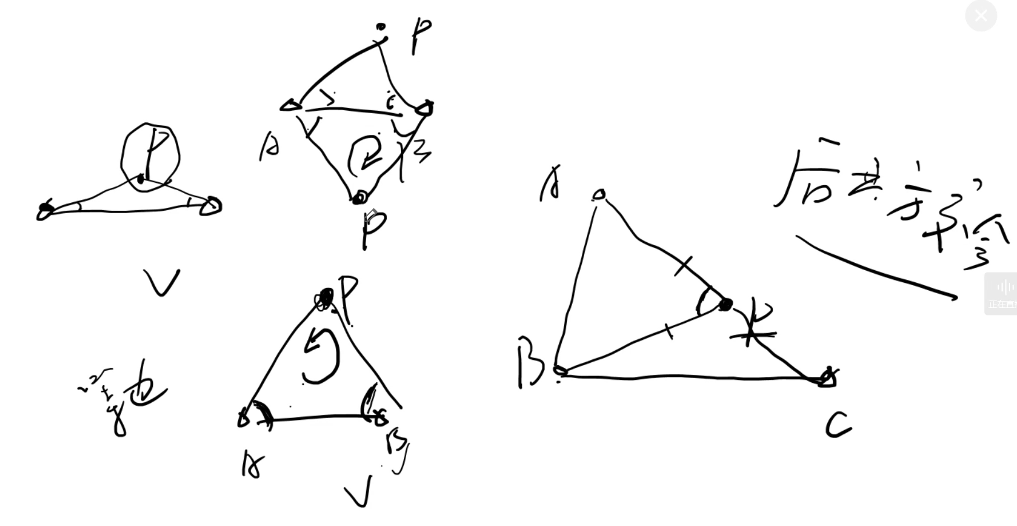
后方交会要注意危险圆!
后方交会有其现实意义
距离交汇
按交汇的图形来分:
- 前方交会
- 测方交会
- 后方交会
按观测值类型分:
- 测角交会
- 侧边交会
- 边角交会
卫星定位方法
- 控制点放到卫星上,测距离——定位置
- 利用卫星信号接受机,同时接受多颗定位卫星发射的信号进行定位,称为卫星定位。
- 每颗卫星播发独立的无线电信号进行距离测量: 距离 = 光速 x 时间
- 为了精确测定时间,卫星上常使用高精度原子钟,GPS 接收机内置较廉价的钟,其计时精度比原子钟的精度低得多,设想一下接收机上钟的误差对距离测定的影响:1/1,000,000 秒的测时误差将引起 300m 的距离误差
- 因此一般需要同时观测 4 颗以上的卫星,求解 3 个坐标参数及 1 个接收机钟差参数
测量工作的原则
- 从整体到局部,先控制后碎部,从高精度到低精度(控制点),逐级加密,层层检核。
- 减小误差积累,保证测图精度
- 可以分幅测绘,加快测图进度
- 防止错漏发生,保证成果正确
什么是小地区?
- 地球曲率对测量工作的影响
- 当测区范围较小时,可以将大地水准面近似当作水平平面看待
- 看作水平面是,需要考虑水平距离和高程影响
- 结论:在半径为 10km 的园内距离,可用切平面代替大地水准面
- 对水平角的影响
- 从球面三角可知,球面上三角形内角之和比平面上相应三角形内角之和多出球面角超 ,其值可用多边形面积求得。
- 当测区范围在 100km2 时,用平面代替水准面时,对角度影响仅为 0.51″,在普通测量工作中可以忽略不计
- 对高差影响
- 在高程测量中,即使距离很短也应考虑地球曲率的影响.
- 参考椭球面是测量计算的基准面










