开始时预习
- 功与能量
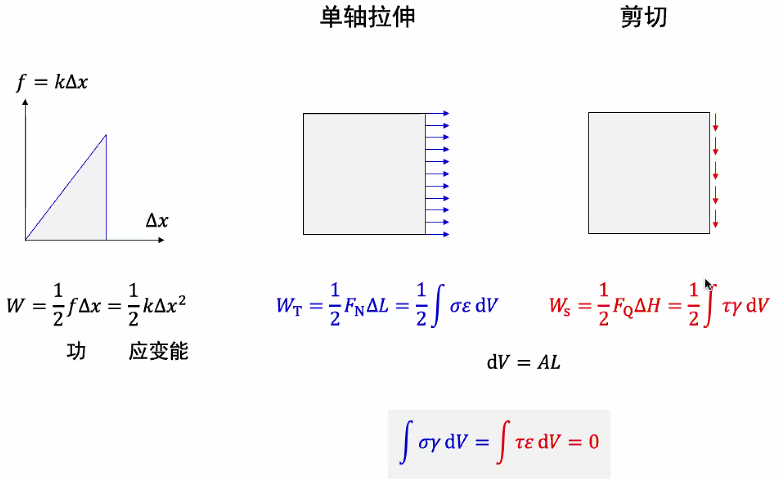
- 准静态加载时,功与应变能如上图所示
- 注意满足的条件!——在其他模态对应的做功为 0,为求解带来了便利
引言
工程上传递功率的圆轴——扭转变形
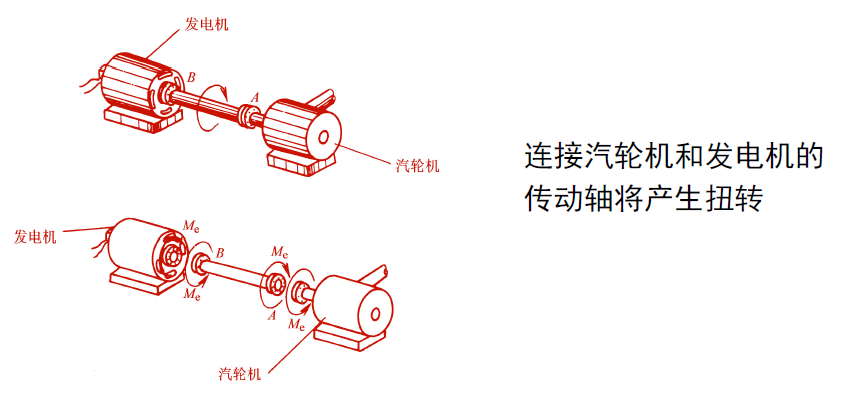
- 例如钻头!
工程上将主要承受扭转的杆件称为轴,当轴的横截面上仅有扭矩 (Mx) 作用时,与扭矩相对应的分布内力,其作用面与横截面重合。这种分布内力在一点处的集度,即为剪应力。圆截面轴与非圆截面轴扭转时横截面上的剪应力分布有着很大的差异。本章主要介绍圆轴扭转时的应力变形分析以及强度设计和刚度设计。
分析圆轴扭转时的应力和变形的方法与分析梁的应力和变形的方法基本相同。依然借助于平衡、变形协调与物性关系。
扭矩和扭矩图
作用在杆件上的外力偶矩,可由外力向杆的轴线简化而得,但是对于传递功率的轴,通常都不是直接给出力或力偶矩,而是给定功率和转速。
因为力偶矩在单位时间内所作之功即为功率,于是有:
$$
M_x\omega = P
$$
其中 Mx为外力扭矩;$\omega$为轴转动角速度;P 为轴传递功率
考虑到: 1 kW = 1000 N·m/s,上式可以改写为
$$
M_x=9549\frac{P}{n}N·m
$$
其中功率 P 的单位为 kW;n 为轴每分钟的转数,用 r/min 表示。
- 注:9549 = 60*1000/2π
例题 1:画出圆轴的扭矩图
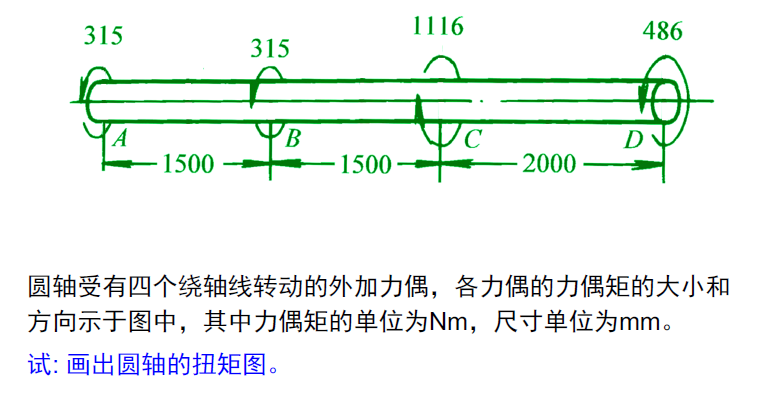
依旧如前——确定控制面——截面法——画图
圆轴扭转剪应力分析
分析圆轴扭转剪应力的方法与下一章分析梁纯弯曲正应力的方法基本相同,就是:
根据表面变形 (待定常数) 作出平面假定;
由平面假定得到应变分布,亦即得到变形协调方程;(单位长度的扭转角关系)
再由变形协调方程与应力-应变关系得到应力分布,也就是含有待定常数的应力表达式;
最后利用静力方程确定待定常数,得到计算应力的公式。
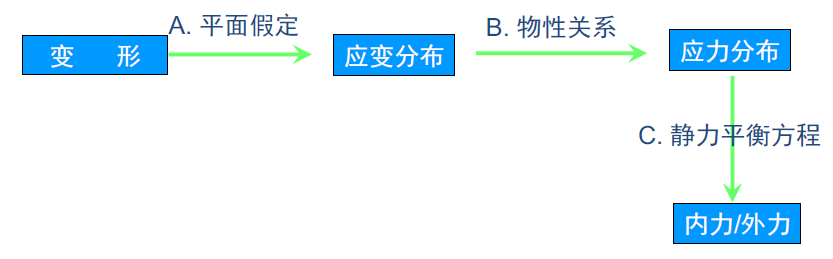
- 在圆轴外侧画上网格——然后看
- 当圆轴承受绕轴线转动的外扭转力偶作用时,其横截面上将只有扭矩一个内力分量。
- 圆轴受扭后,将产生扭转变形 (Twist),圆轴上的每个微元的直角均发生变化,这种直角的改变量即为剪应变。这表明圆轴横、纵截面上都将出现剪应力分别用$\tau$讲$\tau’$表示。
- 圆轴扭转时,其圆柱面上的圆保持不变,都是两个相邻的圆绕圆轴的轴线相互转过一角度。根据这一变形特征,假定:
- 圆轴受扭发生变形后,其横截面依然保持平面,并且绕圆轴的轴线刚性地转过一角度。
- 这就是关于圆轴扭转的平面假定。所谓刚性地转过一角度,就是横截面上的直径在横截面转动之后依然保持为一直线。
变形协调方程
若将圆轴用同轴柱面分割成许多半径不等的圆柱,根据上述结论,在 dx 长度上,虽然所有圆柱的两端面均转过相同的角度$d\theta$,但半径不等的圆柱上产生的剪应变各不相同,半径越小者剪应变越小。

d$\phi$/dx 称为单位长度相对扭转角(twist angle per length)。对于两相邻截面,d $\phi$ /dx 为常数。故上式表明圆轴扭转时,其横截面上任意点处的剪应变与该点至截面中心之间的距离成正比,此为圆轴扭转时的变形协调方程。
若在弹性范围内加载,即剪应力小于某一极限值时,对于大多数各向同性材料,剪应力与剪应变之间存在线性关系。(注意 G 可能不是个常数,所以需要假定小变形)
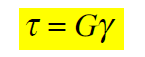
此即为剪切胡克定律(Hooke law in shearing),式中 G 为比例常数,称为剪切弹性模量或切变模量(shearing modulus)。
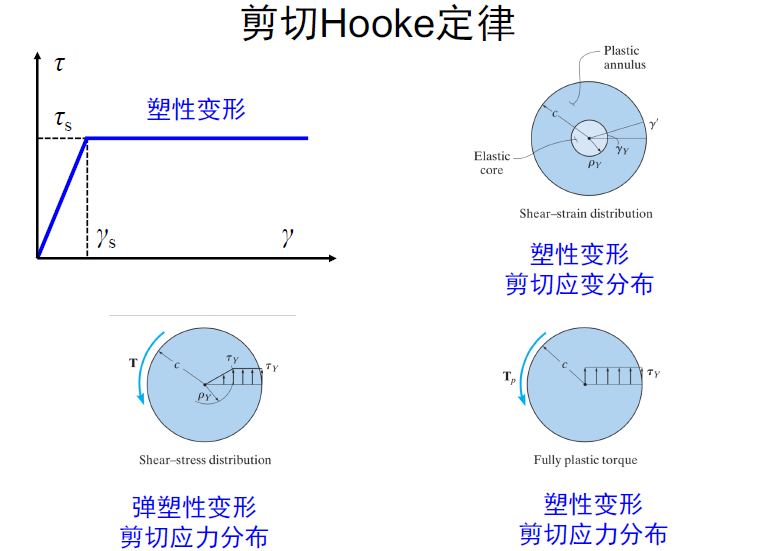
横截面上扭转的剪应力分布是非均匀的!——这与拉伸、剪切不同。
- 为测定剪切时材料的力学性能,需制备扭转试样在扭转试验机上测试。
- 对于
低碳钢 ,采用薄壁圆管或圆筒 进行试验,使薄壁截面上的剪应力接近均匀分布 ,这样才能得到反映剪应力与剪应变关系的曲线。 - 对于
铸铁 这样的脆性材料由于破坏前基本上不发生塑性变形,所以采用实圆截面试样 也能得到反映剪应力与剪应变关系的曲线。 - 试验结果表明低碳钢的剪应力与剪应变关系曲线上,类似于拉伸正应力与正应变关系曲线,也存在线弹性、屈服和破断三个主要阶段。屈服强度和强度极限分别用τs 和 τb 表示。
- 对于铸铁,整个扭转过程都没有明显的线弹性阶段和塑性阶段,最后发生脆性断裂。其强度极限用 τb 表示
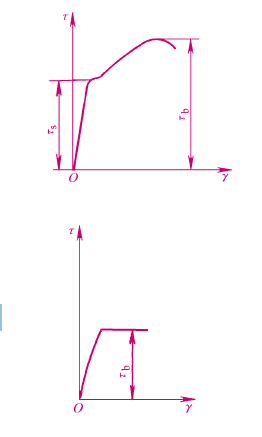
- 韧性材料与脆性材料扭转破坏时,其试样断口有着明显的区别。
- 韧性材料试样最后沿横截面剪断,断口比较光滑、平整。
- 铸铁试样扭转破坏时沿 45 度螺旋面断开,断口呈细小颗粒状。
静力学平衡方程
- 作用在横截面上的剪应力形成一分布力系,这一力系向截面中心简化结果为一力偶,其力偶矩即为该截面上的扭矩。于是有



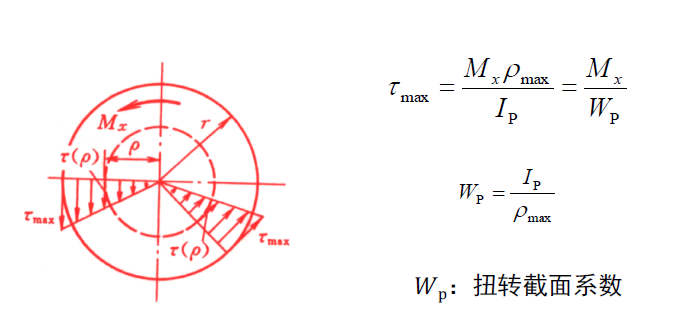

- 其中要注意$\alpha$上为四次方,不要记混
圆轴强度设计
与拉伸强度设计相类似,扭转强度设计时,首先根据扭矩图和横截面的尺寸判断可能的危险截面;然后从危险截面上的应力分布中确定危险点(即最大剪应力作用点);最后利用试验结果直接建立扭转时的强度设计准则。圆轴扭转时的强度设计准则为
$$
\tau_{max}\leq [\tau]
$$
其中[$\tau$]为最大许用剪应力


例题 2:空心轴与实心轴:注重稳定性失效问题,所以不能偏于一点
例题 3:传动机构最大切应力
例题 4:汽车发动机的主传动轴
- 上述结果表明,空心轴远比实心轴轻,即采用空心圆轴比采用实心圆轴合理。将受扭杆件做成空心圆轴,使得横截面中心附近的材料得到充分利用。这是由于圆轴扭转时横截面上的剪应力沿半径方向非均匀分布,截面中心附近区域的剪应力比截面边缘各点的剪应力小得多,当最大剪应力达到许剪应力时,中心附近剪应力远小于许剪应力值。
例题 5:承受扭转的木材,顺纹和横纹许可应力不同,但是剪力互等——所以只需考虑顺纹
扭转角与圆轴刚度设计
扭转刚度计算是将单位长度上的相对扭转角限制在允许的范围内,即必须使构件满足刚度设计准则

- 对于各段扭矩不等或者材料、截面发生改变的轴,扭转角可通过单位长度扭转角积分求得。
例题 6:最大扭矩/最大剪应力
结论与讨论
公式的适用条件
- 不同材质的材料——平面假定依旧成立!
- 应力集中!——应力集中系数
非圆轴截面扭转
- 翘曲:变形特征
- 扭转后,横截面将不再保持平面
- 翘曲使得结构扭转刚度降低
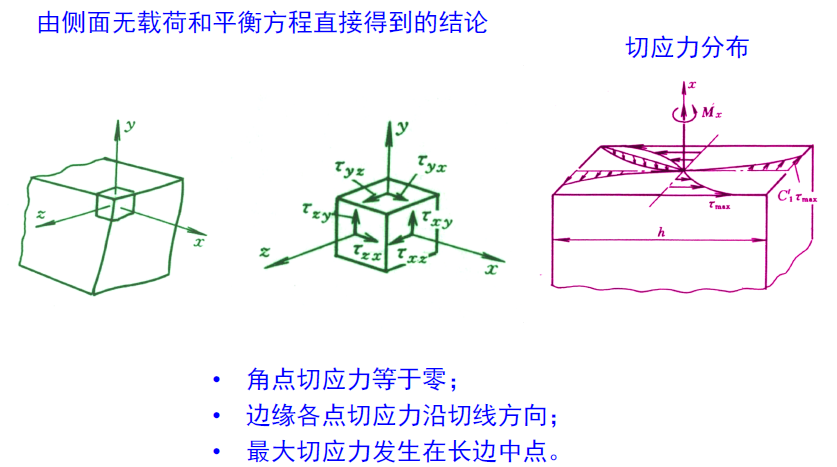
- 有一个有趣的结论
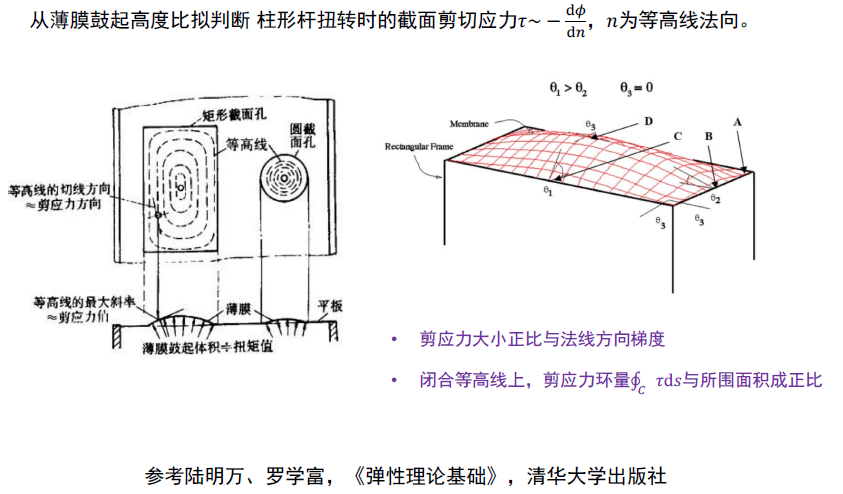
- 充气薄膜——薄膜鼓起高度和剪切应力有关——越陡的地方——剪应力越大
- 对狭长的矩形截面——
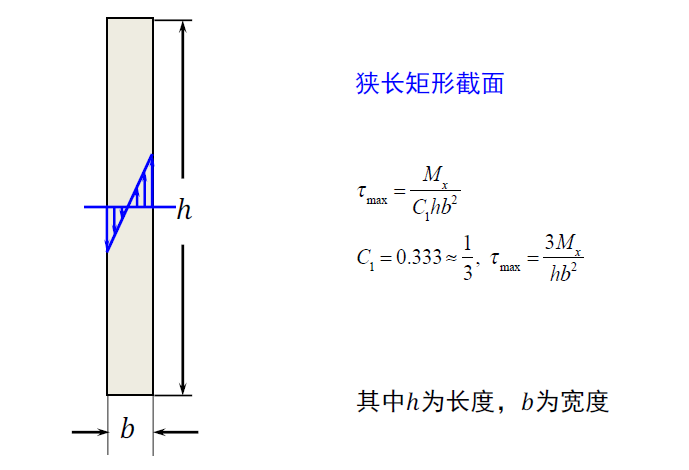
薄壁构件扭转
- 开口薄壁杆件——可以进行剪应力分布——和上面狭长矩形截面相似
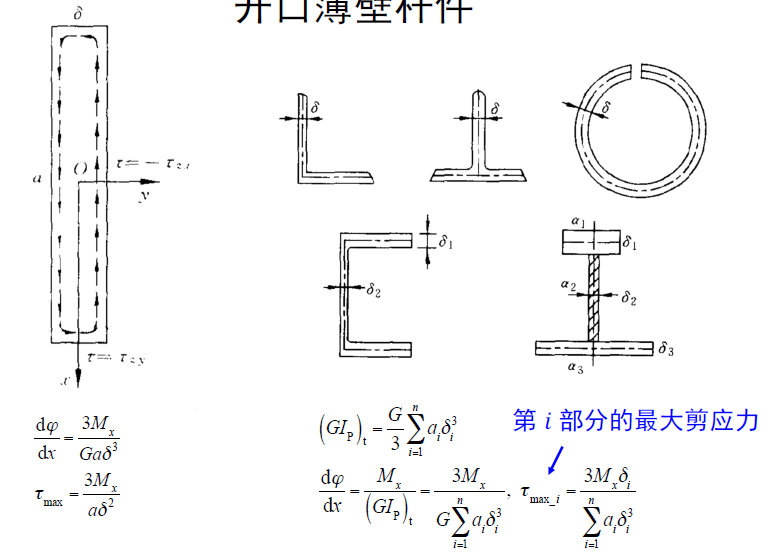
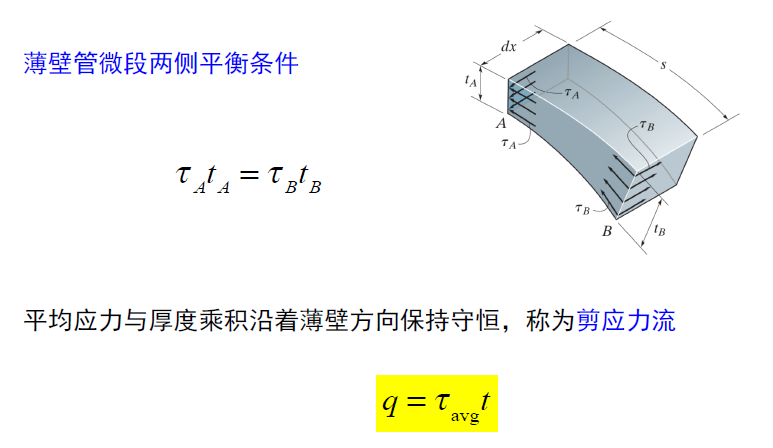
- 闭口薄壁管扭转——剪应力流——两侧平衡

小结











