封面图——张拉结构
二力杆——拉伸或压缩
弯矩线性分布——进行等强度设计时使用杆件比较好
承受轴向载荷的拉压杆在工程中的应用非常广泛。
一些机器和结构中所用的各种紧固螺栓,在紧固时,要对螺栓施加预紧力,螺栓承受轴向拉力,将发生伸长变形。
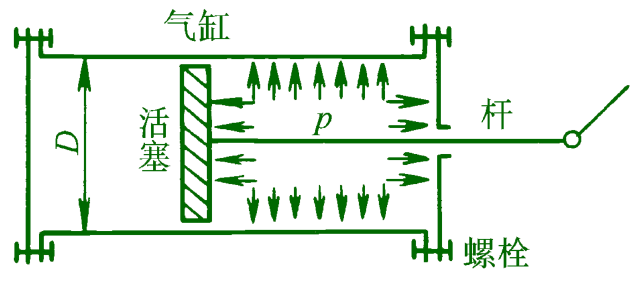
由汽缸、活塞、连杆所组成的机构中,不仅连接汽缸缸体和汽缸盖的螺栓承受轴向拉力,带动活塞运动的连杆由于两端都是饺链约束,因而也是承受轴向载荷的杆件。
悬索桥——拉伸与压缩
拉伸和压缩是杆件基本受力与变形形式中最简单的一种,所涉及的一些基本原理与方法比较简单,但在材料力学中却有一定的普遍意义。
本章主要介绍杆件承受拉伸和压缩的基本问题,包括: 内力、应力、变形、强度设计,材料在拉伸和压缩时的力学性能等,目的是使读者对
此后扭转、弯曲等都要使用这个
轴力与轴力图
沿着杆件轴线方向作用的载荷,通常称为轴向载荷(Normal Load)。杆件承受轴向载荷作用时,横截面上只有轴力$F_N$一种内力分量。
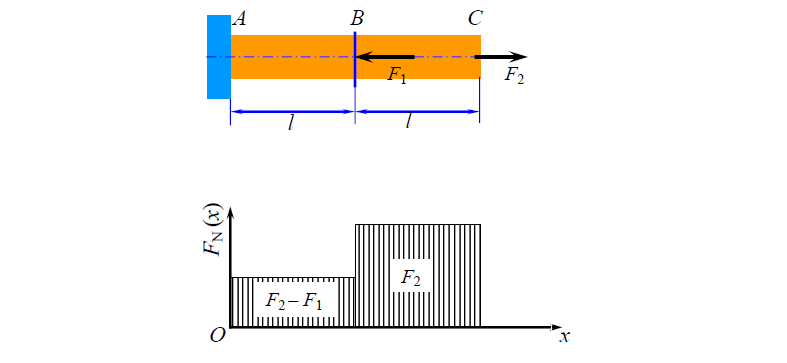
杆件只在两个端截面处承受轴向载荷时,则杆件的所有横截面上的轴力都是相同的。如果杆件上作用有两个以上的轴向载荷,就只有两个轴向载荷作用点之间的横截面上的轴力是相同的。
表示轴力沿杆件轴线方向变化的图形,称为轴力图(Diagram of Normal Force)。
基本概念
- 整体平衡与局部平衡
- 内力与外力的相依关系
- 控制面的选取(集中载荷,突变处设置控制面,如果变化趋势变化,也要设置控制面)
- 杆件内力分量的正负号规则(拉伸为正、压缩为负)
- 指定截面上内力分量的确定
例题 1
:star: 轴力图的绘制
- 确定约束力
- 建立四个控制面,也就是轴力图的分段点
- 然后使用截面法求解控制面上的轴力(画出未知轴力、假设方向,列平衡方程,确定轴力)
- 建立坐标系,画轴力图
拉压杆件中的应力与强度设计
- 这是一个超静定问题
- 当外力沿着杆件的轴线作用时,其横截面上只有轴力一个内力分量。与轴力相对应,杆件横截面上将只有正应力σ。
- 如何知道应力的分布情况?
- 猜——假设是均匀的——平均正应力假设(平均正应变假定)
- $\displaystyle \sigma=\frac{F_{Nx}}{A}$
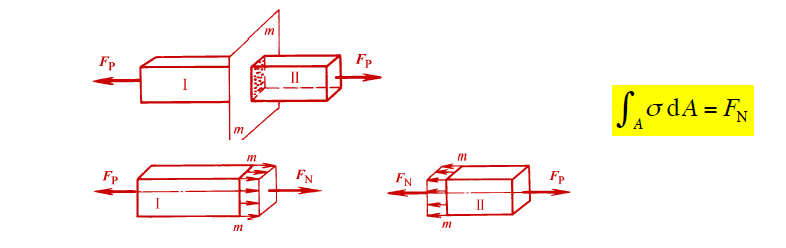
- 考虑不同材质做成的杆件——均匀性不能保证——横截面平行——所以是均匀正应变假定
例题 2
强度设计
- 所谓**强度设计(Strength Design)**是指将杆件中的最大应力限制在允许的范围内,以保证杆件正常工作,不仅不发生强度失效,而且还要具有一定的安全裕度。对于拉伸与压缩杆件,也就是杆件中的最大正应力满足:
$$
\sigma_{max}\leq[\sigma]
$$
- 这一表达式称为拉伸与压缩杆件的强度设计准则(Criterion for Strength Design),又称为强度条件。其中称为许用应力(Allowable Stress),与杆件的材料力学性能以及工程对杆件安全裕度的要求有关,由下式确定
$$
[\sigma]=\frac{\sigma^0}{n}
$$
- 式中σ^0^为材料的极限应力或危险应力(Critical Stress),由材料的拉伸实验确定;n 为安全因数(n>1),对于不同的机器或结构,在相应的设计规范中都有不同的规定。
- 强度计算的依据是强度设计准则或强度条件。据此,可以解决三类强度问题
- 强度校核
- 已知杆件的几何尺寸、受力大小以及许用应力,校核杆件或结构的强度是否安全,也就是验证设计准则是否满足。如果满足,则杆件或结构的强度是安全的;否则,是不安全的。
- 尺寸设计
- 已知杆件的受力大小及许用应力,根据设计准则,计算所需要的杆件横截面面积,进而设计处出合理的横截面尺寸。
- 确定许可载荷
- 根据设计准则,确定杆件或结构所能承受的最大轴力,进而求得所能承受的外加载荷。
- 强度校核
例题 3
螺栓强度校核问题;
吊车许可载荷问题;
使用
拉压杆件的变形
- 两部分变形——沿轴向的变形、横截面面内的变形
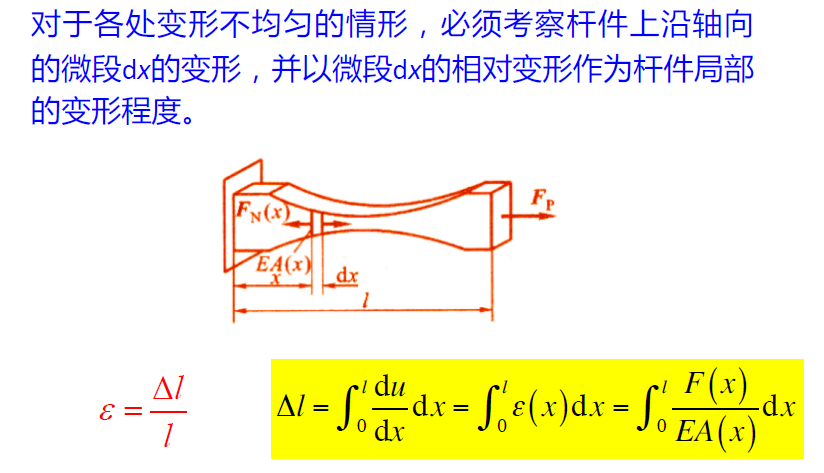
杆件内部承受拉伸、压缩内力时,将产生变形,即伸长、缩短。局部的变形用拉伸、压缩应变描述,而材料的性质反应在内力和变形,或应力与应变之间的关系上,即

- 分为微段,应力、应变都是场变量——应力分量
- 注意其中使用了每一段的变形均相同的假定
- 杨氏模量乘以横截面积——这个值称为拉伸刚度 EA,这与弹簧 k 不同,单位也不同
- 剪切模量乘以面积也可以类似定义
- 模量只与材料有关——而刚度则是材料性质和横截面积
- 当拉、压杆有二个以上的外力作用时,需要先画出轴力图,然后按上式分段计算各段的变形,各段变形的代数和即为杆的总伸长量(或缩短量):
- 杆件承受轴向载荷时,除了轴向变形外,在垂直于杆件轴线方向也同时产生变形,称为横向变形。
- 轴向应变与横向应变存在关系
$$
\epsilon_y = - \nu\epsilon_x
$$
- 在一个方向上有载荷——在其他方向也会有反应
- 在弹性力学中会有一个证明$-1\leq \nu \leq 0.5$
- 大部分材料的ν为正值。杆件单轴拉伸允许横向变形时应力应变之比为 Young’s 模量。

- 拉胀材料——负泊松比现象

- 使用一张揉皱的纸也可以制造出负泊松比材料
泊松比为什么范围是-1~0.5?
体积模量 B 与剪切模量 G,利用这些来进行求解
例题 4
见讲义
拉压时材料的力学性能
其中σ0 为材料的极限应力或危险应力。所谓危险应力是材料发生强度失效时的应力。**这种应力不是通过计算,而是通过材料的拉伸实验得到的。**通过拉伸实验一方面可以观察到材料发生强度失效的现象,另一方面可以得到材料失效时的应力值。
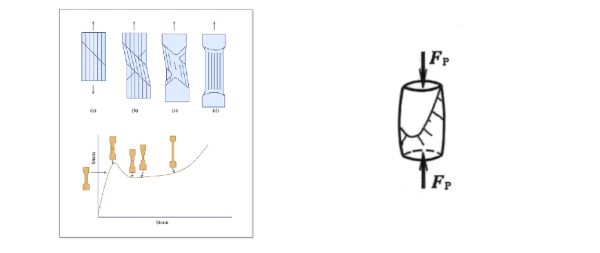
材料拉伸时的应力应变曲线
- 电子万能试验机
- 进行拉伸实验,首先需要将被试验的材料按国家标准制成标准试样(Standard Specimen),然后将试样安装在试验机上,使试样承受轴向拉伸载荷。通过缓慢的加载过程,试验机自动记录下试样所受的载荷和变形,得到应力与应变的关系曲线,称为应力-应变曲线(Stress-Strain Curve)。
- 试验时,试样通过卡具或夹具安装在试验机上。试验机通过上下夹头的相对移动将轴向载荷加在试样上。
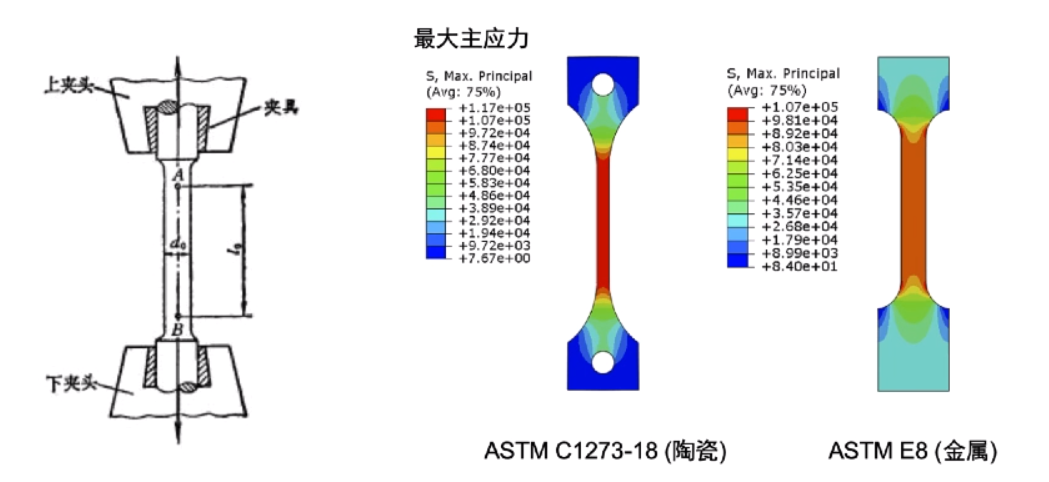
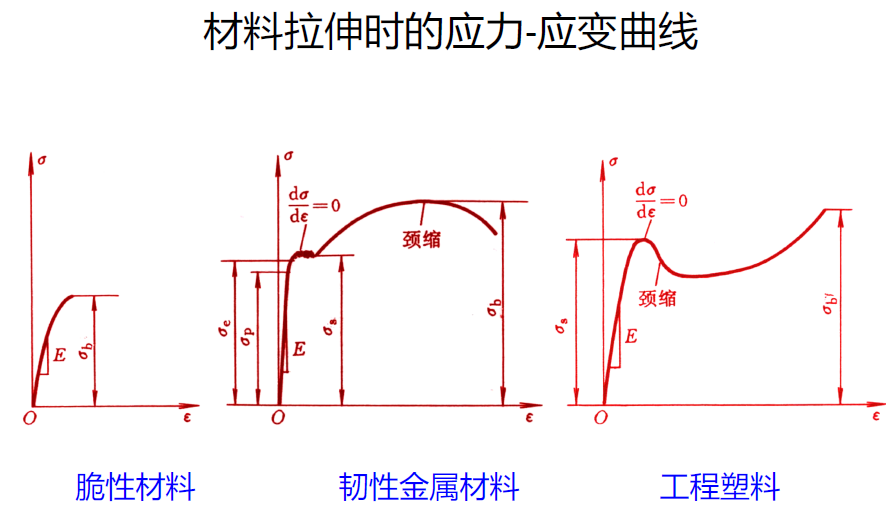
脆性材料拉伸时的力学性能
- 开始时软化,此后就直接断裂——变软了
- 例如铸铁
- 对于脆性材料,从开始加载直至试样被拉断,试样的变形都很小。而且,大多数脆性材料拉伸的应力-应变曲线上,都没有明显的直线段,几乎没有塑性变形,也不会出现屈服和颈缩现象,因而只有断裂时的应力值,即强度极限。
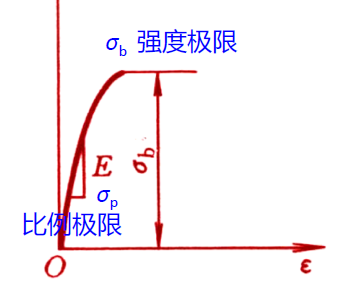
- 关心两个数——杨氏模量和强度极限 b——brick
韧性材料拉伸时的力学性能
- 应力应变曲线中的直线段称为线弹性阶段。弹性阶段中的应力与应变成正比,比例常数即为材料的弹性模量 E。对于大多数韧性材料,其应力-应变曲线上没有明显的直线段,铸铁的应力-应变曲线即属此例。因为没有明显的直线部分,常用割线的斜率作为这类材料的弹性模量,称为割线模量。
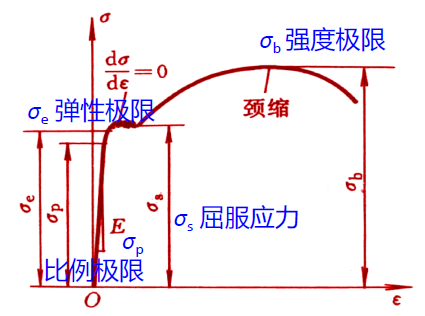
- 应变较大——韧性
- 变形过程中能够吸收很多能量——线性
- 比例极限——拟合出来——杨氏模量
- 弹性极限——还是弹性变形
- 比例极限与弹性极限
- 应力应变曲线上线弹性阶段的应力最高限称为比例极限(Proportional Limit),用σP 表示。线弹性阶段之后,应力-应变曲线上有一小段微弯的曲线,这表示应力超过比例极限以后,应力与应变不再成正比关系,但是,如果在这一阶段,卸去试样上的载荷,试样的变形将随之消失。这表明这一阶段内的变形都是弹性变形,因而包括线弹性阶段在内,统称为弹性阶段。弹性阶段的应力最高限称为弹性极限(Elastic Limit),用表示。大部分韧性材料比例极限与弹性极限极为接近,只有通过精密测量才能加以区分。
- 屈服应力
- 许多韧性材料的应力-应变曲线中,在弹性阶段之后,出现近似的水平段(dσ/dε = 0),这一阶段中应力几乎不变,而变 形急剧增加,这种现象称为屈服(Yield)。这一阶段曲线的最低气的应力值称为屈服应力或屈服强度(Yield Stress),用$\sigma_s$表示。
- 对于没有明显屈服阶段的韧性材料,工程上则规定产生 0.2%塑性应变时的应力值为其屈服应力,称为材料的条件屈服应力(Offset Yield Stress),用$\sigma_{0.2}$表示。
- 强度极限
- 应力超过屈服应力或条件屈服应力后,要使试样继续变形,必须再继续增加载荷。这一阶段称为强化(Strengthening)阶段。这一阶段应力的最高限
称为强度极限(Strength Limit),用表示。
- 应力超过屈服应力或条件屈服应力后,要使试样继续变形,必须再继续增加载荷。这一阶段称为强化(Strengthening)阶段。这一阶段应力的最高限
- 某些韧性材料(例如低碳钢和铜),应力超过强度极限以后,试样开始发生局部变形,局部变形区域内横截面尺寸急剧缩小,这种现象称为
颈缩 (Necking)。出现颈缩之后,试样变形所需拉力相应减小,应力一应变曲线出现下降阶段,直至试样被拉断。

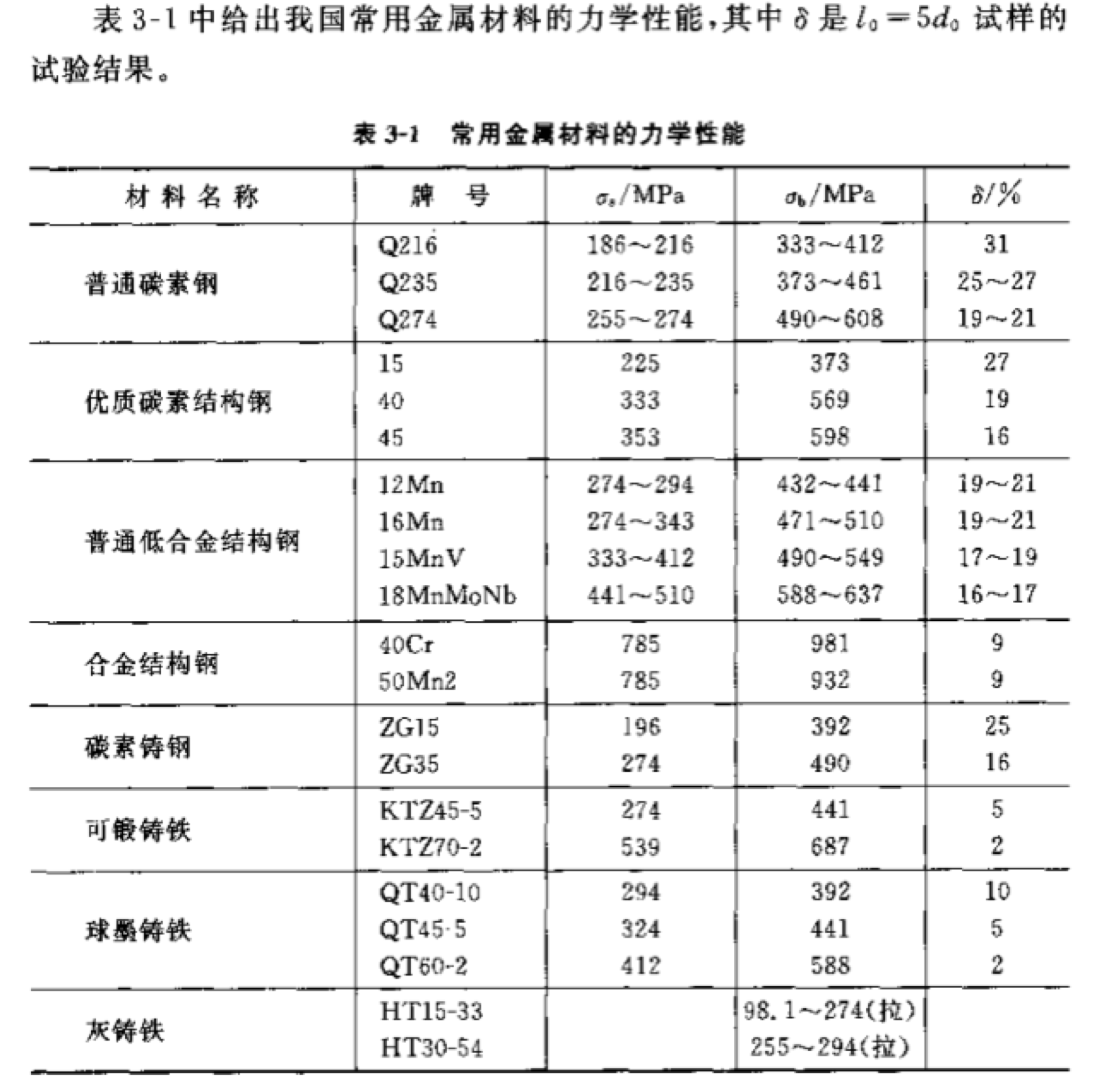
- 注意其中的 Q235
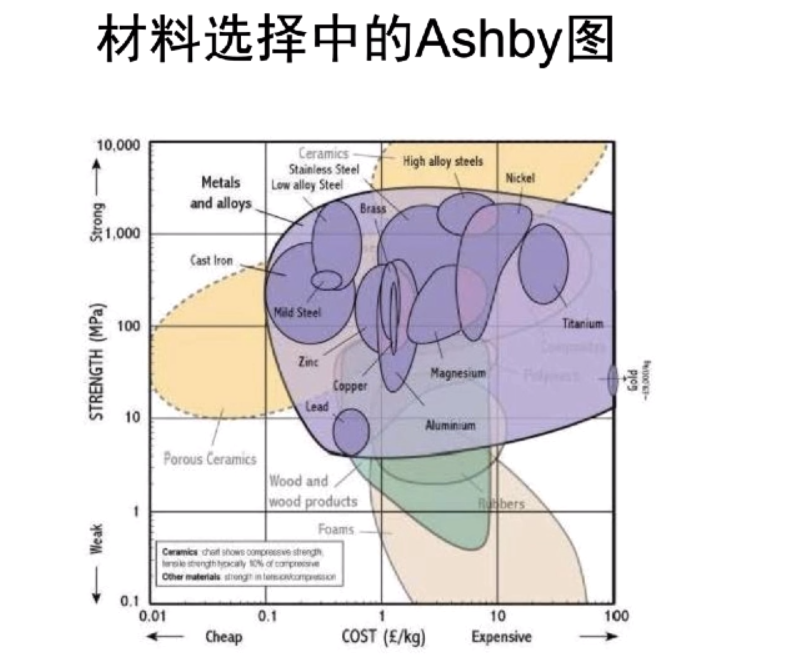
- 材料选择中的 Ashby 图
强度失效概念与失效应力
略
压缩时材料的力学性能
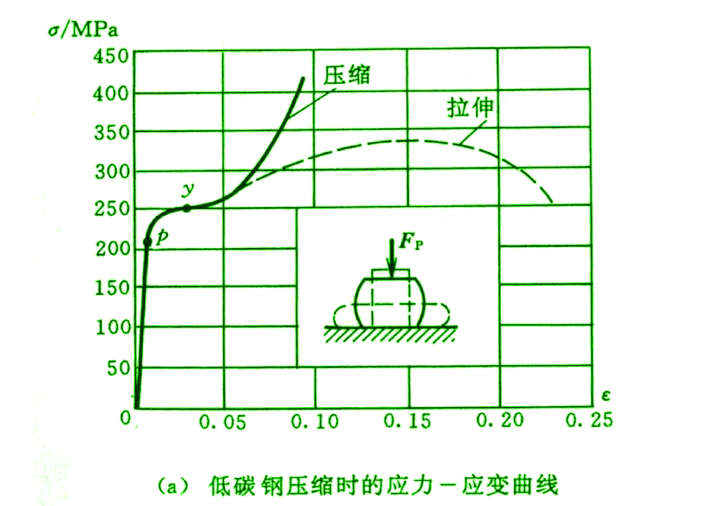
上图是韧性材料
而脆性材料如下图:
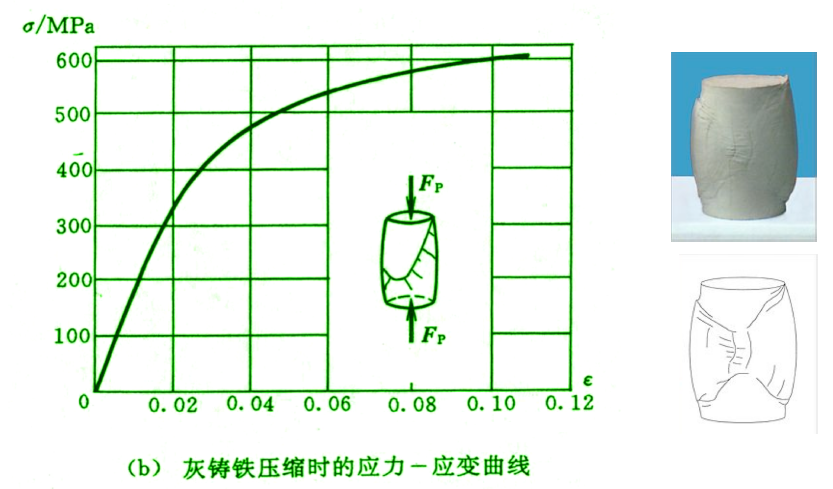
- 在弹性阶段,杨氏模量还是适用的
卸载的力学行为
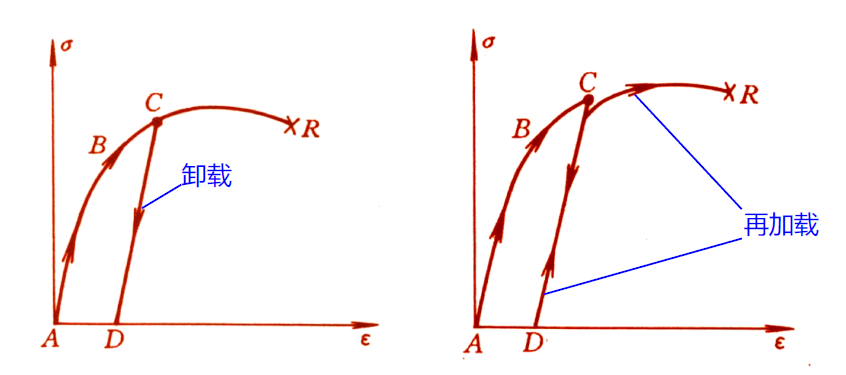
- 有残存塑性变形
结论与讨论
应力和变形公式的应用条件
怎样从受力或内力判断杆件沿轴向方向均匀变形是均匀的呢?
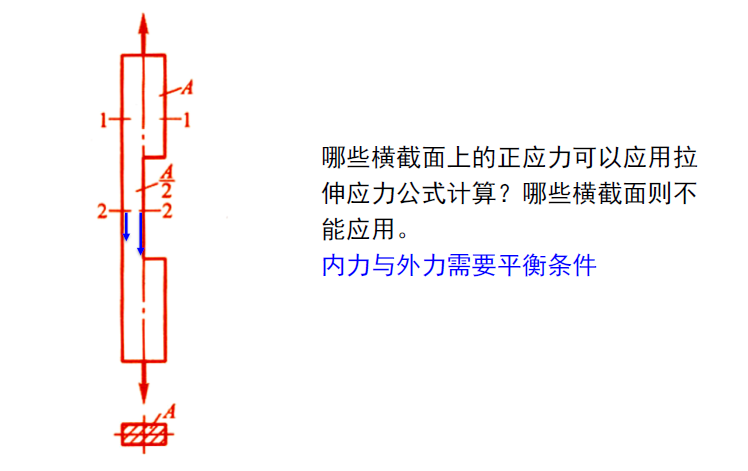
- 2-2 截面必然有应变的改编
- 平面沿着平行方向移动——认为合理
- 具体问题具体分析——涨落可以认为不计(材料大小远大于涨落时)
- 对于变形公式
- 应用时有两点必须注意:
- 导出这一公式时应用了 Hooke 定律,因此只有杆件在弹性范围内
加载时,才能应用上述公式计算杆件的变形; - 公式中的 FNx 为一段杆件内的轴力,只有当杆件仅在两端受力时
FNx 才等于外力 FP。
- 导出这一公式时应用了 Hooke 定律,因此只有杆件在弹性范围内
- 当杆件上有多个外力作用,则必须先计算各段轴力,再分段计算变形然后按代数值相加。
- 应用时有两点必须注意:
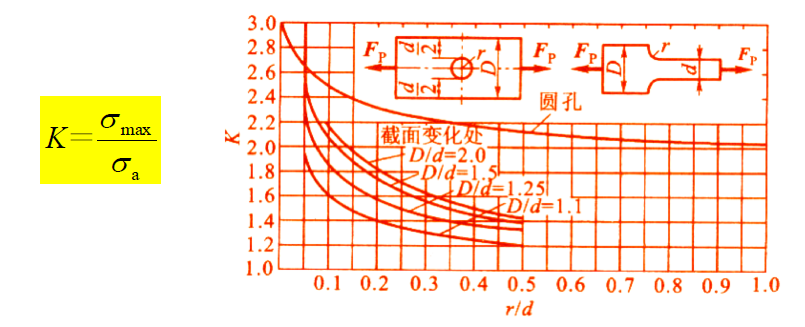
应力集中
几何形状不连续处应力局部增大的现象,称为
应力集中的程度用应力集中因数描述。应力集中处横截面上的应力最大值与不考虑应力集中时的应力值(称为名义应力)之比,称为
热应力、残余应力与生长应力
- 热应变:非外载引起的本征应变,若几何受限则产生应力。
- 如何求解?
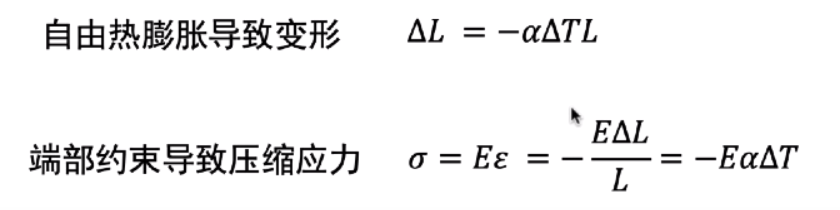
- 生长应力:树、草等等受力
- 失配应力:硅锗合金
- 残余应力:非弹性变形
- 本征应力/Eshelby 夹杂问题
- 椭球区域——应力均匀分布
- 外载作用下因材料非均匀性引起的附加应变/应力。
超静定问题
静定问题与静定结构
- 未知力(内力或外力)个等于独立的平衡方程数
超静定问题与超静定结构
- 未知力个数多于独立的平衡方程数
超静定次数 - 未知力个数与独立平衡方程数之差
- 多余约束 - 保持结构静定多余的约束
静定与超静定的辩证关系
- 多余约束的两种作用:增加了未知力个数,同时增加对变形限制与约束,前者使问题变为不可解,后者使问题变为可解。
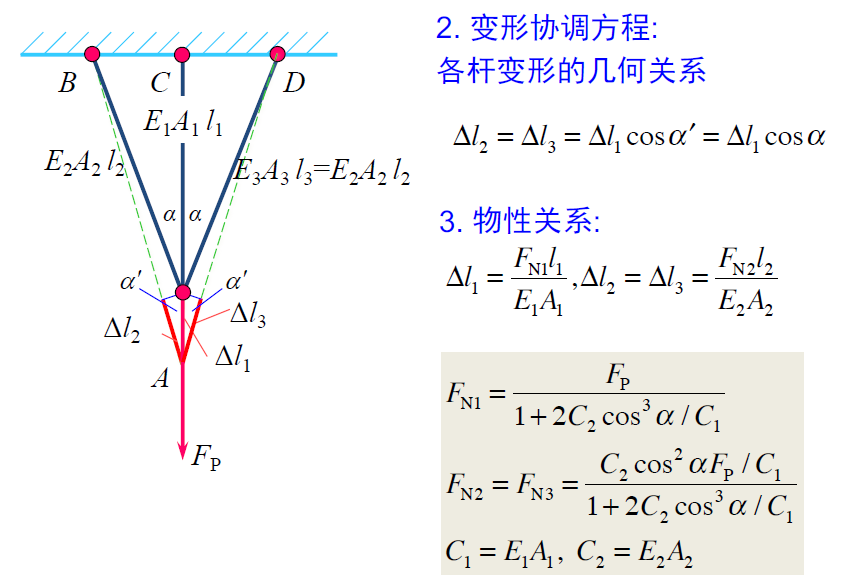
求解超静定问题的基本方法
- 平衡、
变形协调 、物性关系 。现在的物性关系体现为力与变形关系。
超静定结构的妙用:
- (1) 贝聿名的杰作
- (2) 钢筋混疑土结构的优化设计
例题 6
见讲义
叠加法
要求——根据控制方程的特点可知当载荷与变形之关系为
先释放约束,再逐一考虑各项约束——满足总变形量为 0
截面上的力
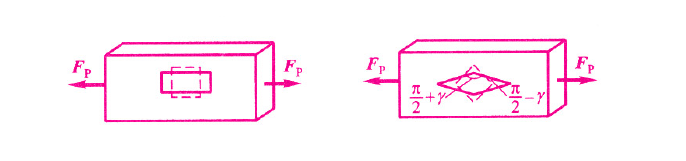
受力后,正置小方块的直角并未发生改变,而斜置小方格变成了菱形,直角发生变化。这种现象表明,在拉、压杆件中,虽然横截面上只有正应力,但在斜截面方向却产生剪切变形,这种剪切变形必然与斜截面上的切应力有关。
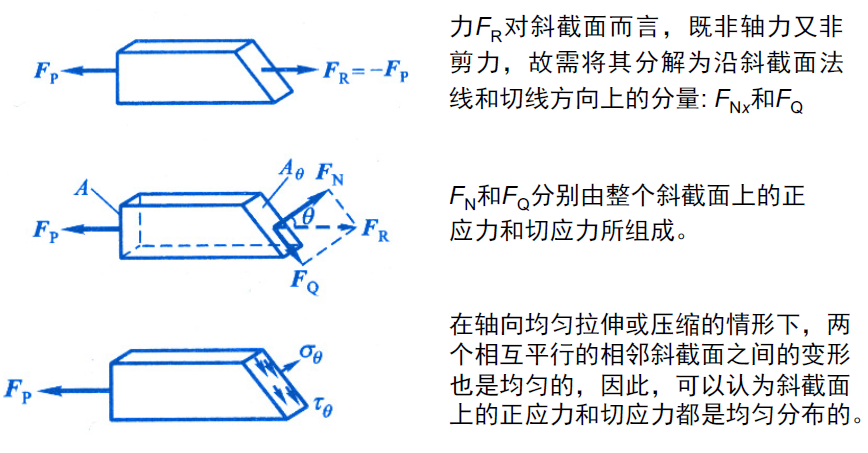
- 为确定拉(压)杆斜截面上的应力,可以用假想截面沿斜截面方向将杆截开,斜截面法线与杆轴线的夹角设为θ。考察截开后任意部分的平衡,求得该斜截面上的总内力
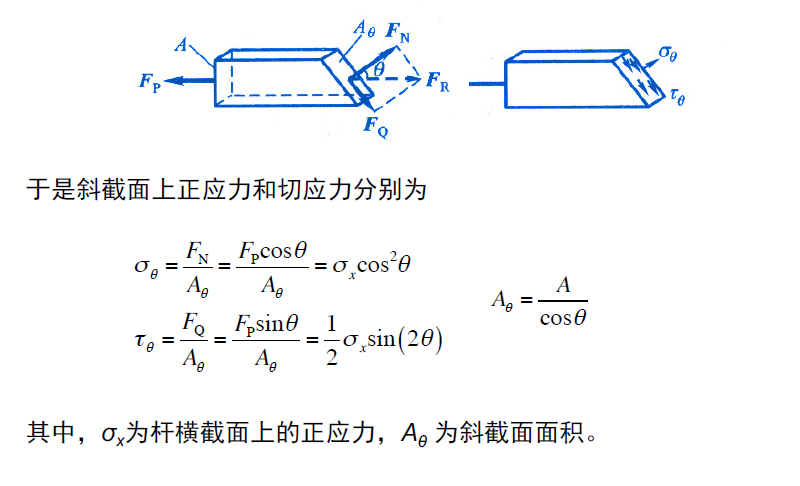
- 注意:其有周期性!!
- 或者还可以使用其他方法:
- 拉压杆斜截面上的应力公式也可通过考察杆件上的微元求得。以相距很近的两横截面和两纵截面从杆内截取微小单元体,简称微元。所取微元只有左、右面上受有正应力σx。
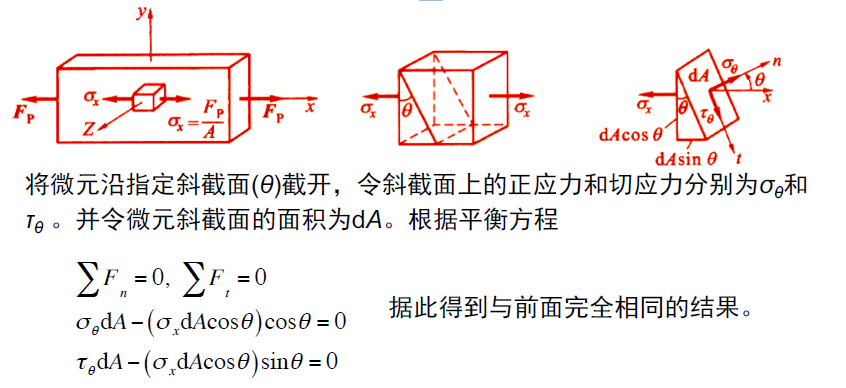
- 上述结果表明,杆件承受拉伸或压缩时,横截面上只有正应力;斜截面上则既有正应力又有切应力。而且,对于不同倾角的斜截面,其上的正应力和切应力各不相同。

- 为什么需要讨论这个?
- 由于微元取得很小,上述微元斜面上的应力,实际上就是过一点处不同方向面的应力。因此,当论及应力时,必须指明是
哪一点处 、哪一个方向面上的应力。 - 脆韧性材料的破坏准则?
- 低碳钢拉伸至屈服时,表面出现 45o 滑移线,由切应力引起错动滑移。灰铸铁拉伸时沿横截面断开,由拉伸断裂导致。灰铸铁压缩至破坏沿 55o 错动破坏。