梁的位移分析的工程意义
位移分析中所涉及的梁的变形和位移,都是弹性的。尽管变形和位移都是弹性的,工程设计中,对于结构或构件的弹性位移都有一定的限制。弹性位移过大,也会使结构或构件丧失正常功能,即发生刚度失效。
工程设计中还有另外一类问题,所考虑的不是限制构件的弹性位移,而是希望在构件不发生强度失效的前提下,尽量产生较大的弹性位移。例如,各种车辆中用于减振的板簧 (Leaf Spring),都是采用厚度不大的板条叠合而成,采用这种结构,板簧既可以承受很大的力而不发生破坏,同时又能承受较大的弹性变形,吸收车辆受到振动和冲击时产生的动能,受到抗振和抗冲击的效果。
上一章中已经提到,如果忽略剪力的影响,在平面弯曲的情形下,梁的轴线将弯曲成平面曲线,梁的横截面变形后依然保持平面,且仍与梁变形后的轴线垂直。由于发生弯曲变形,梁横截面的位置发生改变,这种改变称为位移。位移是各部分变形累加的结果。位移与变形有着密切联系,但又有严格区别。有变形不一定处处有位移;有位移也不一定有变形。这是因为,杆件横截面的位移不仅与变形有关,而且还与杆件所受的约束有关。在数学上,确定杆件横截面位移的过程主要是积分运算,积分限或积分常数则与约束条件和连续条件有关。
基本概念

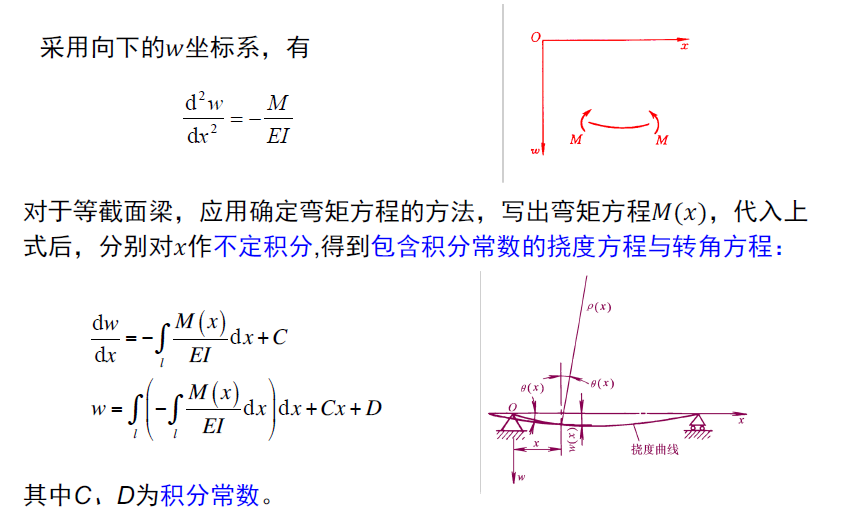
小挠度微分方程及其积分
- 挠度曲线——挠曲线
- 梁在弯曲变形后,横截面的位置将会发生改变
- 这种位置的改变称为位移
- 包括挠度、转角、轴向位移(弦)

例题 1:悬臂梁
例题 2:简支梁
积分法小结:
- 确定约束力,判断是否需要分段以及分几段
- 分段写出弯矩方程
- 分段建立挠度微分方程
- 微分方程的积分
- 利用约束条件和连续条件确定积分常数
- 确定挠度与转角方程以及指定截面的挠度与转角
工程中的叠加法
在很多的工程计算手册中,已将各种支承条件下的静定梁,在各种典型载荷作用下的挠度和转角表达式列出,简称为挠度表。
基于杆件变形后其轴线为一光滑连续曲线和位移是杆件变形累加的结果这两个重要概念,以及在小变形条件下的力的独立作用原理,采用叠加法 (Superposition Method) 由现有的挠度表可以得到在很多复杂情形下梁的位移。
例题 3:简支梁受多种载荷
逐段刚化法
简单的静不定梁
求解静不定梁.除了平衡方程外,还需要根据多余约束对位移或变形的限制,建立各部分位移或变形之间的几何关系,即建立几何方程,称为变形协调方 程 (Compatibility Equation),并建立力与位移或变形之间的物理关系,即物理方程或称本构方程 (Constitutive Equations)。将这二者联立才能找到求解静不定问题所需的补充方程。
据此,首先要判断静不定的次数,也就是确定有几个多余约束;然后选择合适的多余约束,将其除去,使静不定梁变成静定梁,在解除约束处代之以多余约束力;最后将解除约束后的梁与原来的静不定梁相比较,多余约束处应当满足什么样的变形条件才能使解除约束后的系统的受力和变形与原来的系统弯曲等效,从而写出变形协调条件。
例题 4:静不定 1
例题 5:静不定 2,对称性
梁的刚度设计
- 对于主要承受弯曲的零件和构件,刚度设计就是根据对零件和构件的不同工艺要求,将最大挠度和转角 (或者指定截面处的挠度和转角) 限制在一定范围内,即满足弯曲刚度设计准则 (Criterion for Stiffness Design):
例题 6:求解转角的值
结论与讨论
变形与位移
- 总体的变形是微段变形累加的结果,有位移不一定有变形
梁的连续光滑曲线
- 由约束性质及连续光滑性确定挠曲线的大致形状及位置
提高刚度
- 增加惯性矩
- 选用 E 更高的材料
- 减小梁的长度
斜弯曲
……










