工程力学总论

复习

• 杆件中的小孔会对其刚度、强度、稳定性作何影响？

• 强度最敏感，为什么？

• 因为强度是一个极值的概念，而刚度和稳定性是一个平均的概念

• 弯曲——整体的变形，刚度——K 的变化

• 强度取决于整个杆件中最弱的部分

• 刚度失效——力和变形之间的关系

• 强度失效——发生断裂

• 稳定性失效——发生突然的变形模式转变

工程力学总论

工程力学的基本概念

• 力系平衡
  • 比萨斜塔——重力与支撑力
  • 需要一个合力和合力矩，说明塔基具有一个不均匀的力
  • 产生两种破坏模式——左侧箭头为负值——断裂——倒塌
  • 右侧增大——压折——难于承受
• 应力状态
  • 力分布的不均匀性如何描述？
  • 拉纸——摩擦阻力——拉断——在手捏的地方发生断裂——纸受力程度不同——理想情况下力的分布是均匀的，但是实际上并不均匀——力的最大集度必然大于平均集度——这被成为应力集中
  • 实验——在纸上剪孔，拉伸——合力相同，横截面积变小——应力集中
  • 应力：单位面积上的力，如图
  • 描述在何处、何种方式破坏
• 变形
  • 变形体中相对位置会发生改变——位移场表示
  • 场变量——$w \propto L^3$
  • 如果有一堆小鸟？——$w \propto L^4$
• 刚度
  • 对于相同结构讲——不锈钢>木材，相同材料讲——
  • Galilei——木材的实验，相同的重力，刚度小——变形大
  • 刚度：力与变形之间的关系
• 强度与韧性
  • fracture of bones——骨头是一个脆性材料
  • 而韧性材料则会产生塑性变形
  • 脆性材料断裂——粗糙、锋利的断层
  • Titanic 发生断裂——沉没前
  • US Navy collision——碰撞仅是产生了变形
  • 韧性与材料、温度有关
  • 材料脆韧性改变——材料力学研究的问题
  • 脆性——陶瓷——强度高
  • 韧性——金属——释放很大的能量
• 稳定性
  • 失效的一种模式——911 事件——大厦上部有一段呈现竖直向下的移动——稳定性的丧失
  • 失稳——重力势能的释放——对整个楼的倒塌是十分重要的一步
• 失效
  • 工程构件（泛指结构元件、机器零件和部件等）在外力作用下丧失正常功能的现象称为失效或破坏（failure）
  • 强度失效、刚度失效、稳定性失效
  • 疲劳失效——在交变应力下发生了失效
  • 别针——产生塑性变形——内部结构发生改变——多几个回合——发生交变应力——产生越来越多的损伤——强度越来越低，产生了疲劳破坏失效——灾难性的失效模式
  • 航空事件——多与结构件失效相关

工程力学的研究模型

工程设计的过程：

为了完成常规工程设计任务，需要进行以下工作：

• 分析并确定构件所受各种外力的大小和方向（工程静力学）
• 研究在外力作用下构件的内部受力、变形和失效的规律（材料力学）
• 提出保证构件具有足够强度、刚度和稳定性的设计准则和设计方法（设计手册）

实际工程构件受力后、几何形状和几何尺寸都要发生改变——称为变形——构件称为变形体

在研究其受力时、在大多数情形下——变形很小——忽略这种变形并不会产生什么影响——所以在工程静力学中可以看作是一个 刚体

比如研究塔吊——可以看作是刚体——塔式吊车起吊重物后——杆件发生变形——研究其刚度、强度、稳定性失效需要使其为 变形体

• 从几何上讲——可以分为杆、板、壳、块体等几类

• 对不同的几何形状、几何尺度，场函数的复杂度不同

• 某一方向比其他两个方向上的尺寸大的多——杆

  • 受载条件——梁（受弯）、轴（扭转）、柱（压、拉）

  • 轴线直线——直杆，反之——曲杆

  • 截面尺寸相同——等截面杆，反之，变截面杆

  • 若构件在某一方向尺寸比其余两个方向上的尺寸小得多，为平面形状者称为板(plates)；为曲面形状者称为壳(shells)，穹形屋顶、化工容器等均属此类。

  • 若构件在三个方向上具有同一量级的尺寸，则称为块体构物基础等均属此类。

工程力学的分析方法

• 理论分析方法

  • 工程静力学——在变形前的构件上进行受力分析
  • 材料力学——研究力和变形之间的关系
  • 关于变形前构形的讨论
    • 小变形假定可避免几何非线性
  • 从确定的 M 计算 w

• 工程力学的实验分析方法

  • 伽利略做木梁弯曲试验的装置（木梁左侧端点的破环）
  • 拉伸试验机——做成试样——然后进行拉伸——测量点的距离、力等等——构件的设计——上下两端都很大——使材料在中间部分破坏——狭长段的应力相对均匀
  • 初始距离——应力，应变
  • 载荷很小——应力应变是线性的
  • 飞机静载试验
  • 汽车疲劳试验

• 计算分析方法

  • 离散化方法

  • 分而治之，把不均匀的结构化成小方块——求解每个小方块的应力

  • 结构拓扑优化——根据鸟喙设计机翼——3D 打印机翼——强度、刚度提升但不显著增加重力

小结

材料力学=材料+力学

结构材料指具有足够受力能力的材料。它不仅被用于制造飞船、潜艇，承载人类上天入海的梦想，也被用来建造房屋，制造汽车、家用器具等日常用品。力学行为之于材料，特别是结构材料，正如流动之于水，热之于火，是主要特征，也是性能保障的基础。在人们不断追求更强材料的过程中，对于材料力学行为的研究由来已久。从 1755 年现代混凝土的发明到 1856 年被誉为工业文明基石的钢铁材料的大吨位冶炼技术出现，从 1807 年弹性模量的提出到 1934 年位错机制的诞生，这些材料科技史上的重大时刻无一不与人们对材料力学行为的需求和研究进展有关。

材料在不同加载条件下呈现出多样的力学行为，包括弹性变形、塑性 变形、加工硬化、蠕变、疲劳、断裂等。载荷的大小与加载方式 (拉、压、扭转、弯曲等)、速率、梯度、环境温度等均会影响材料的力学响应，而这些响应又与材料的化学、晶体结构、微结构单元、相组成等 显微组织密切相关。因而，材料力学行为的研究内容丰富。近年来， 一些新型结构材料的出现更是极大地拓展了材料力学行为研究的内涵，为材料力学行为研究开辟了新空间，带来了新机遇。

——《材料力学行为》序——卢柯

介绍了基本概念：力、变形、力学失效模式

基本考虑：材料、结构和功用

研究方法：理论，实验与模拟；刚体与变形体模型

后序：结构力学、结构力学

材料力学基本概念

研究内容与历史

• 材料力学的研究对象——弹性体——除平衡问题外，涉及到变形——以及力和变形之间的关系
• 此外，由于变形，在材料力学中还将涉及到弹性体的失效以及与失效有关的设计准则。
• 将材料力学理论和方法应用于工程，即可对杆类构件或零件进行常规的静力学设计，包括强度、刚度和稳定性设计。

材料力学中变形的概念

• 在工程静力学中，忽略了物体的变形，将所研究的对象抽象为刚体。实际上，任何固体受力后其内部质点之间均将产生相对运动，使其初始位置发生改变，称之为位移(displacement)，从而导致物体发生变形(deformation)。

• 位移的偏导

• 工程上，绝大多数物体的变形均被限制在弹性范围内，即当外 加载荷消除后，物体的变形随之消失，这时的变形称为弹性变 形(elastic deformation)，相应的物体称为弹性体(elastic body)。

材料力学的历史

• 15、16 世纪：da Vinci 的早期实验
  • 钢丝拉伸试验：研究强度和刚度
  • 测量力、位移
• 17 世纪： Galileo 拉伸、弯曲试验，Hooke 定律
  • 拉伸试验，右侧是弯曲梁弯曲试验
  • 每个横截面上弯矩的大小
  • 横截面上最大应力和距离二次方成正比
  • 变形与运动之间的关系——拉伸与压缩
  • $\displaystyle E = E_0 + c\Delta x + \frac{1}{2} k \Delta x^2 + d \Delta x^3+\cdots$
  • $\displaystyle f=-\frac{\partial E}{\partial \Delta x} = - c - k \Delta x - 3d \Delta x^2+\cdots$
• 18 世纪：Euler 曲线，材料力学的工程应用
  • 弹性线的情况——一定情况下解决弹性杆件的问题
  • 弹性杆件问题——在一定的情况下有解析解
• 19 世纪：数理弹性，Navier, Cauchy, Saint-Venant
  • 在固体上提出微元的概念
  • 借助水力学的概念
  • Saint-Venant 原理——局域化的载荷只会发生在很小的范围内
  • 如果研究细长杆件可以认为是均匀的
• 20 世纪：材料特性，破坏、损伤与断裂，计算方法
  • 疲劳、损伤、弹性、塑性
  • 在断裂之前可以吸收很大的能量——但是有大部分是非弹性的——原子回复产生的运动——变形不可恢复，发生颈缩（剪切变形）
  • 判定横截面改变量
  • 脆性断裂有规则断面
• 21 世纪：新材料，工程优化设计

基本假定

1. 材料

• 均匀连续性假定
• 各向同性假定

2. 变形

• 小变形假定
• 变形协调假定
• 所谓假定，即为未作特殊说明时的情形，在具体应用中并不一定合理。

关于材料的基本假定：

• 组成构件的材料，其微观结构和性能一般都比较复杂。研究构件的应力和变形时，如果考虑这些微观结构上的差异，不 仅在理论分析中会遇到极其复杂的数学和物理问题，而且在 将理论应用于工程实际时也会带来极大的不便。为简单起见，在材料力学中，需要对材料作了一些合理的假定。
• 忽略微观，均匀化
• 均匀连续性假定
  • 假定材料无空隙、均匀地分布于物体所占的整个空间。从微观结构看，材料的粒子当然不是处处连续分布的，但从统计学的角度看，只要所考察的物体之几何尺寸足够大，而且所考察的物体中的每一“点”都是宏观上的点，则可以认为物体的全部体积内材料是均匀、连续分布的。
  • 根据这一假定，物体内的受力、变形等力学量可以表示为各点坐标的连续(场)函数，从而有利于建立相应的数学模型。
  • 微观上不连续。宏观连续
  • 高分子链、官能团、等等
• 各向同性假定(Isotropy)
  • 假定弹性体在所有方向上均具有相同物理和力学性能。根据这 一假定，可用一个参数描写各点在各个方向上的某种力学性能。大多数工程材料虽然微观上不是各向同性的，例如金属材料， 其单个晶粒呈结晶各向异性(Crystallographic Anisotropy)，但 当它们形成多晶聚集体的金属时，呈随机取向，因而在宏观上表现为各向同性。
  • 高分子——纤维——尺度很大——那么就可以认为是各向同性的

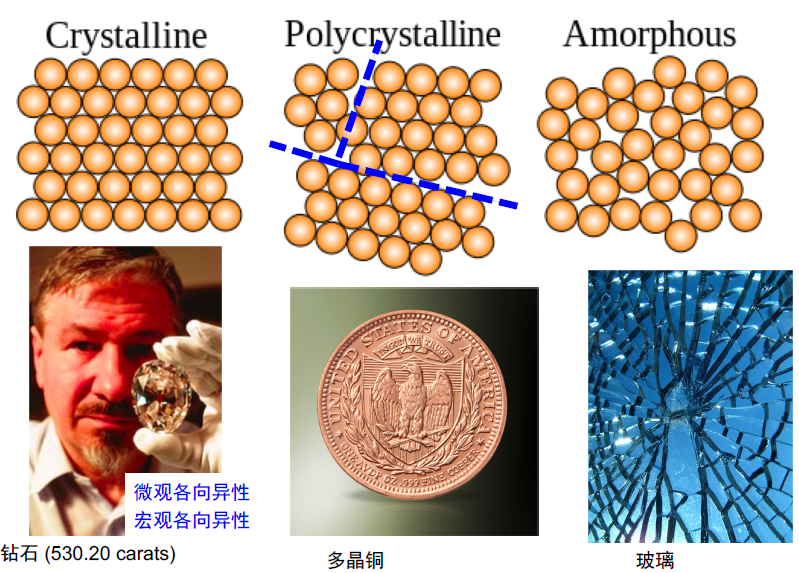
• 微观上各向异性、宏观上各向同性
• 两机：航空发动机、燃气轮机
• 早期——多晶——发生蠕变？——产生损伤——后续——定向晶体——减少蠕变
• 加载力后多久能看到变形？加载变形多久能看到力？
• 弹簧——为 0，如果是湿面团——具有粘弹性——发生蠕变
• 当然如果是金属材料——温度升高——也会产生蠕变
• 单晶各向异性塑性变形

关于变形的基本假定：

• 在采用数学方法解决材料变形问题时，往往会因为材料性能或者变形方式引起非线性，给解析求解带来困难。因而在材料力学框架下，我们往往对材料性质和结构的变形模式作一些合理的假定，以简化分析过程。
• 小变形假定
  • 假定物体在外力作用下所产生的变形与物体本身的几何尺寸相比是很小的。根据这一假定，当考察变形固体的平衡问题时， 一般可以略去变形的影响，因而可以直接应用工程静力学方法。
  • 不难发现，在工程静力学中，实际上已经采用了上述关于小变 形的假定。因为实际物体都是可变形物体，所谓刚体便是实际 物体在变形很小时的理想化，即忽略了变形对平衡和运动规律 的影响。从这个意义上讲，在材料力学中，当讨论绝大部分平衡问题时，仍将沿用刚体概念，而在其它场合，必须代之以变 形体的概念。此外，以后的分析中还会发现，小变形假定在分析变形几何关系等问题时将使问题大力简化。

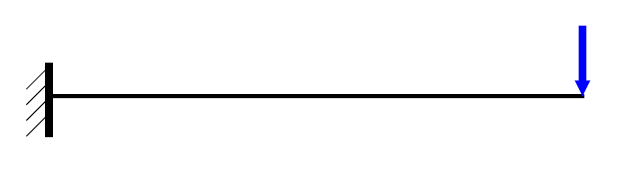
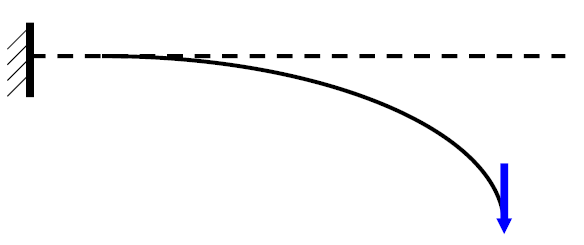
• 考虑几何改变对弯矩的影响
• 大变形状态——柔性电子——硅片变薄——悬臂梁——有转动需要讨论
• 变形协调假定
  • 在材料力学中我们避免讨论力学载荷作用下材料微观结构超越弹性变形范围的变化，例如断裂、塑性变形等，为此在外力作用下，弹性体的变形应当使弹性体各相邻部分既不断开，也不
    重叠。

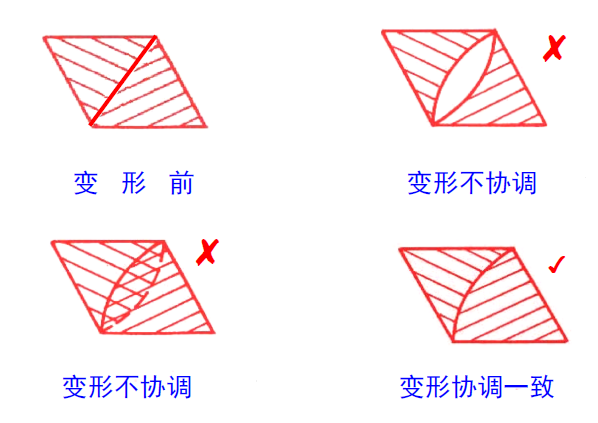
风载（补充）

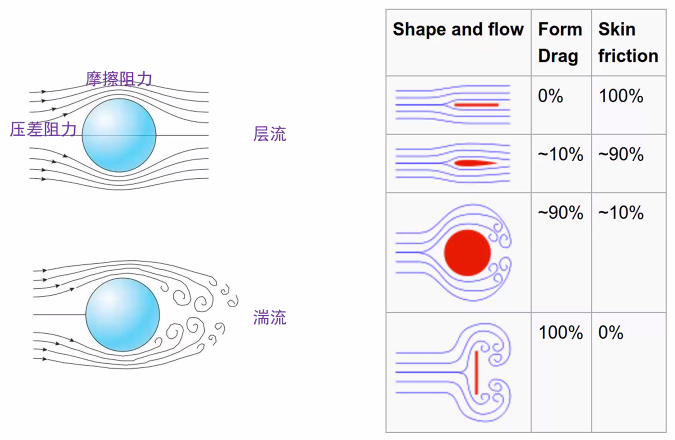
• What is?
• 风载来源于两个方面——压差阻力
• 计算：冲量定理

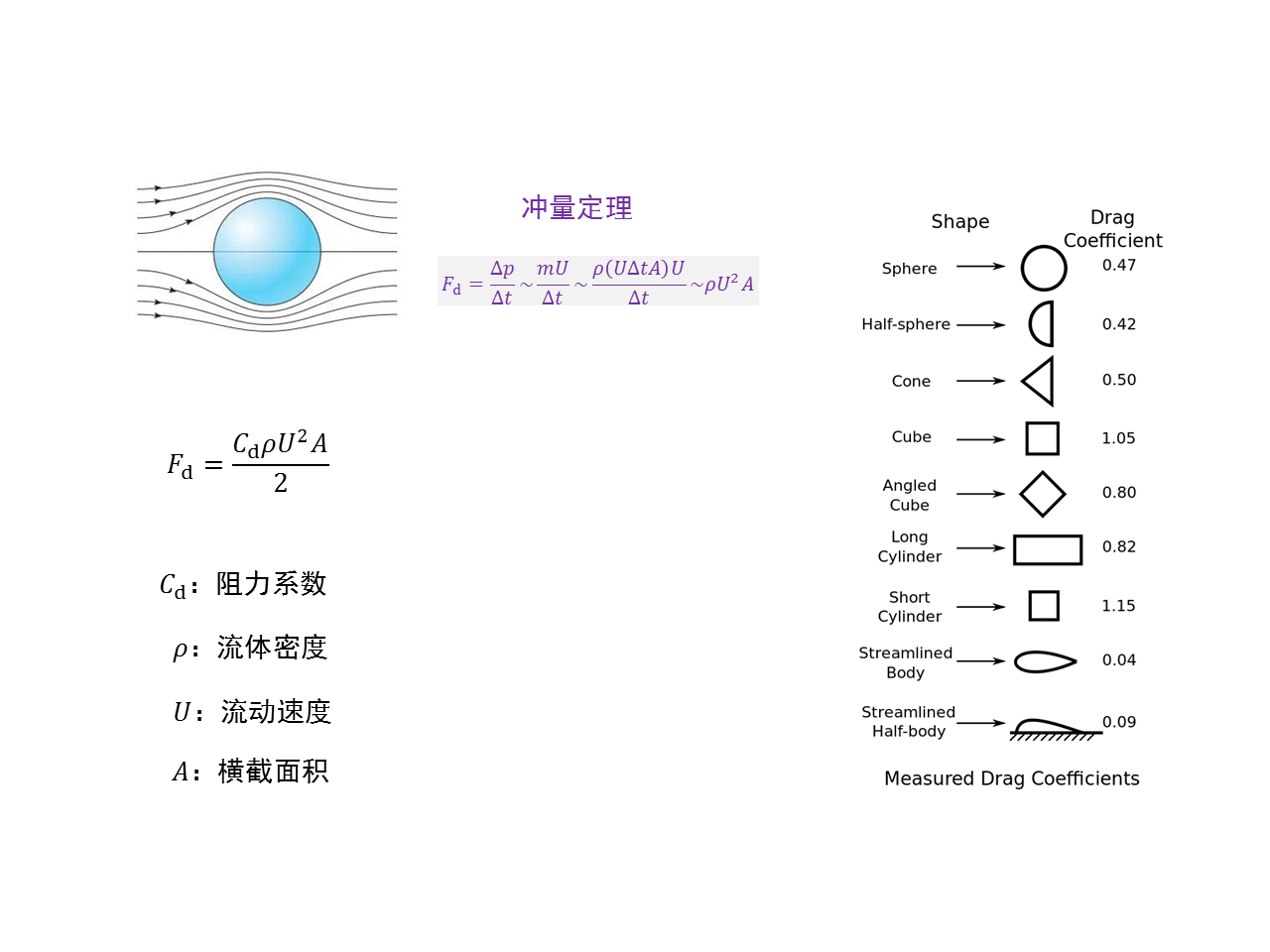
• 如何求 Cd

• Reynolds 数

强度、刚度、稳定性失效（补充）

• 失稳的临界载荷更小
• 塑性变形的临界载荷更小
• 工程——失效曲线——包含弹性和塑性

变形特征与受力分析

弹性体受力与变形特征

• 由于整体平衡的要求，对于截开的每一部分也必须是平衡的。因此，作用在每一部分上的外力必须与截面上分布内力相平衡，组成平衡力系。这是弹性体受力、变形的第一个特征。
• 弹性体受力后发生的变形也不是任意的，必须满足协调 (Compatibility)一致的要求。这是弹性体受力、变形的第二个特征。
• 弹性体的内力分量与变形有关，不同的变形形式对应着不同的内力分量。

外力

• 包括外加载荷和约束力
• 外力分为体积力和表面力，简称体力和面力
• 体力分布于整个物体内，并作用在物体的每个质点上
• 面力是研究对象周围物体直接作用在其表面上的力。根据面力作用区域的大小，可简化为集中力和分布力。实际中集中力是理想化的——作用面积忽略不计，而作用面积相对大——分布力
• 此处力是广义的——包括力和力矩
• 约束力根据运动约束类型可包含力和力矩部分。

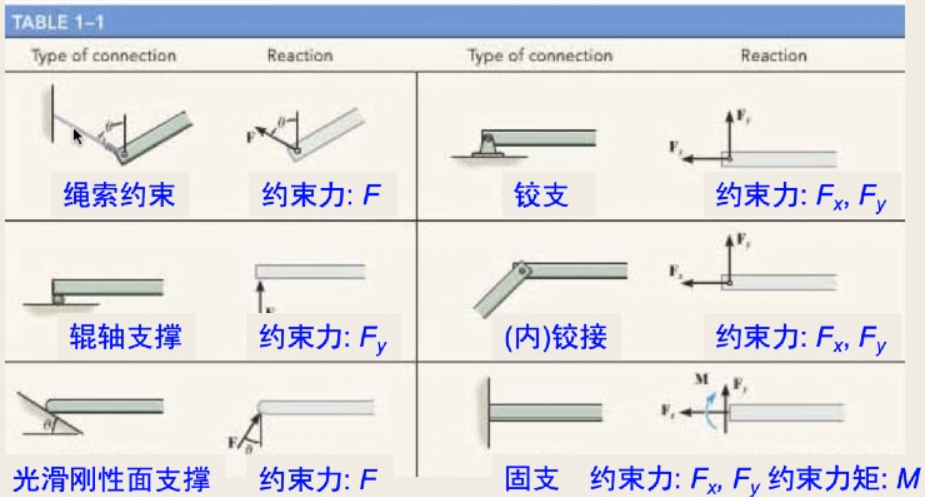
• 对于任意力系，根据主矢和主矩表达式

• 外力与内力——梁和拉杆谁先破坏？
• 梁将远先于拉杆发生破坏，而且二者的变形形式也是完全不同的。可见，在材料力学中不仅要分析外力，而且要分析内力。

截面法——基于内力的分析方法

• 为了揭示承载物体内的内力，通常采用截面法。
• 这种方法是，用一假想截面将处于平衡状态下的承载物体截为 A, B 两部分。为了使其中任意一部分保持平衡，必须在所截的截面上作用某个力系，这就是 A, B 两部分相互作用的内力。
• 根据牛顿第三定律，作用在 A 部分截面上的内力与作用在 B 部分同一截面上的内力在对应的点上，大小相等、方向相反。
• 根据材料的连续性假定，作用在截面上的内力应是一个连续分布的力系。 在截面上内力分布规律未知的情形下，不能确定截面上各点的内力。(静不定问题)
• 但是应用力系简化的基本方法，这一连续分布的内力系可以向截面形心简化为一主矢 F~R~和主矩 M，再将其沿三个特定的坐标轴分解，便得到该截面上的 6 个内力分量 。
• 内力分量

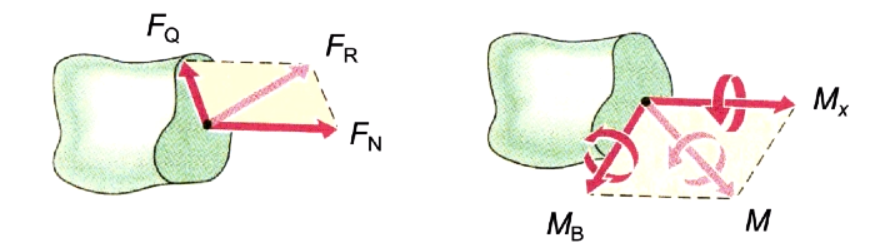
• 正交坐标轴中——法向力称为轴力（轴向伸长/缩短）
• 剪力——剪切变形
• 轴向力矩——扭矩
• 面内力矩——弯矩

截面法：

• 应用平衡方法，考察所截取的任意一部分的平衡，即可求得杆件横截面上各个内力分量的大小和方向。

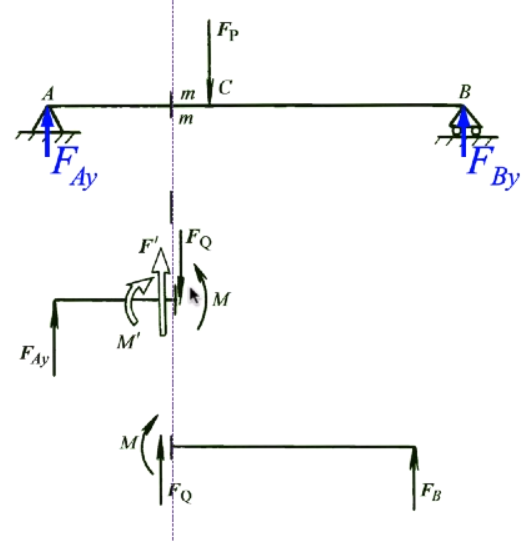
• 方向规定！
• 注意：只在结构变形中才会用到，在讨论外力时依然使用坐标轴
• 轴力——无论作用在哪一侧截面上，使杆件受拉者为正；受压者为负。
• 扭矩——扭矩矢量方向与截面外法线方向一致者为正；反之为负。
• 剪力——使截开部分杆件产生顺时针方向转动者正；逆时针方向转动者负。
  需注意此定义与 x 轴正方向定义（左／右）有关。
• 弯矩——作用在左侧面上使截开部分顺时针方向转动；或者作用在右侧截面上使 截开部分逆时针方向转动者为正；反之为负。
  注意此定义与 y 轴方向选择（上/下）有关。
• 截面可否取在受力处？——不可以，利用连续性
• 小结
  • 首先应用工程静力学方法，确定作用在杆件上的所有未知的外力。(利用刚体模型假设)
  • 在所要考察的横截面处，用假想截面将杆件截开，分为两部分。(避开集中力作用点或者分布力间断处)
  • 考察其中任意一部分的平衡，在截面形心处建立合适的直角坐标系，由平衡方程计算出各个内力分量的大小与方向。
  • 考察另一部分的平衡，以验证所得结果的正确性。

例题：参见讲义内容

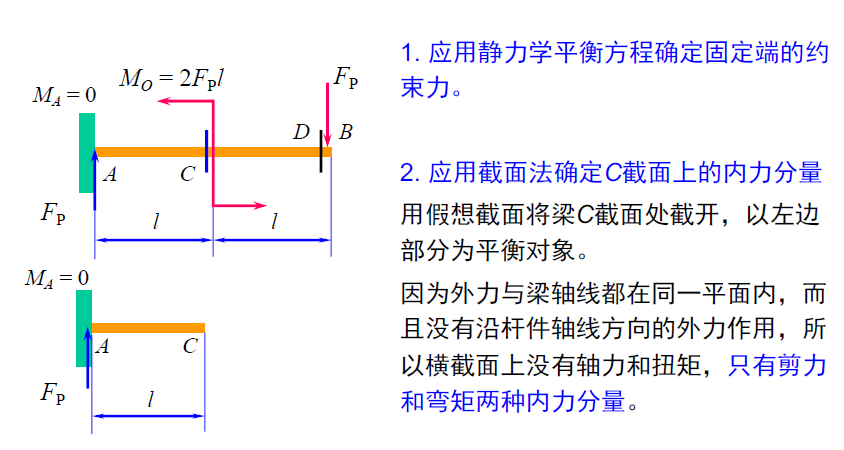
应力和应变

分布？——一些假定——否则就是静不定问题

正应力与剪应力

• 应力就是单位面积上的内力。
• 工程构件，大多数情形下，内力并非均匀分布，集度的定义不仅准确而且重要，因为破坏或失效往往从内力集度最大处开始。
• 如何定义破坏/失效准则?

应力的定义基于我们将材料假设为连续介质(Continuum)，即包括密度等在内的材料性质都在空间中连续分布，然而随着物理尺度的减小，材料的非连续性，例如材料中的缺陷(通常在 10^-6^米尺度及其以下)以及原子的离散性(~10^-10^米)将使得这一假设变得不合理。

值得庆幸的是，今年来的研究发现连续介质力学，甚至是材料力学中的一些概念和公式可以成功应用到纳米尺度(即 10^-9^- 10^-7^米)的材料中，并进行定量地描述。

作为一个公理，我们接受了这一作为通则的原理，然而这只不过是一个基本的简化。没有一个充分的理由来解释为什么曲面面元 dS 两面物质作用力的力矩一定为零。有人曾提出一个广义 Euler-Cauchy 应力原理，引入偶应力(Couple stress)的概念，但是其可实际应用的领域较少。

• 不考虑偶应力
• 工程上多用 MPa
• 一般情形下的横截面上的分布内力，总可以分解为两种：作用线垂直于截面的；作用线位于横截面内的。分布内力在一点的集度，称为应力(Stress)。作用线垂直于截面的应力称为正应力(Normal Stress)，用希腊字母σ表示；作用线位于截面内的应力称为切应力或剪应力 (Shear Stress)，用希腊字母τ表示。应力的单位记号为 Pa 或 MPa，工程上多用 MPa。
• 为什么？Pascal——如果将砖块放入深海——受压——压应变
• 模量大约是 1GPa，1%所有伸长所以根据数量级是 10MPa
• 微分定义

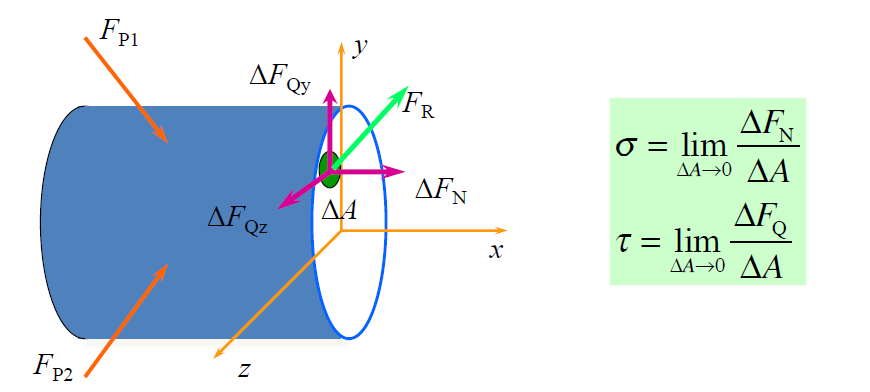
• 希腊字母正应力$\sigma$，剪应力$\tau/\sigma$，正应变$\epsilon$，剪应变$\gamma$，泊松比$\nu$，材料的密度$\rho$

• 第一个下标表示面，第二个表示方向

• 应力做积分——内力

• 应力乘以力矩积分——力矩

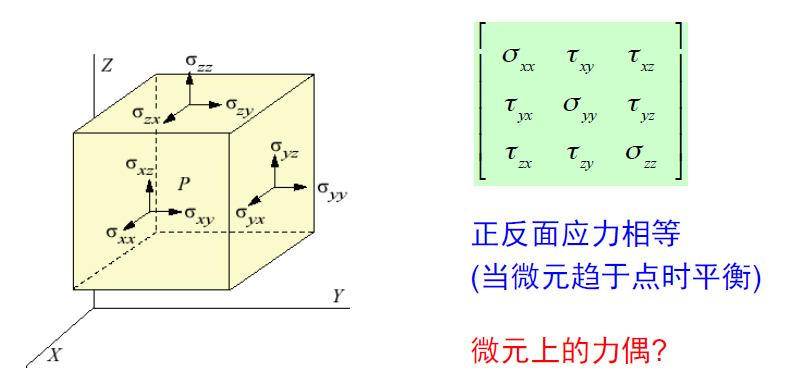
注意两个下标！

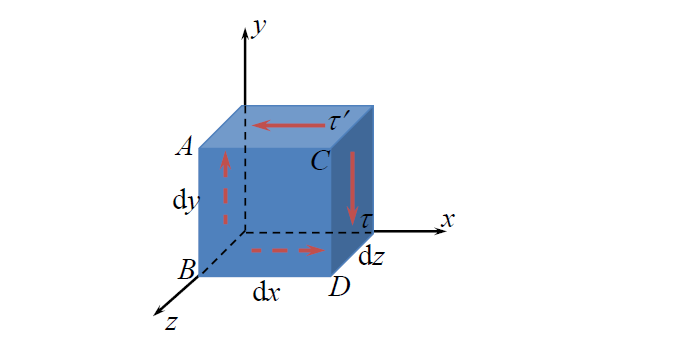
$$
\Sigma M=\tau’dxdydz-\tau dxdydz=0
$$

$$
\displaystyle\tau_{xy}=\tau_{yx},\tau_{xz}=\tau_{zx},\tau_{yz}=\tau_{zy}
$$

• 因此应力矩阵是对称矩阵

• 这与之前杆的应力的方向是不同的
• 讨论微元是满足剪应力互等的两个应力相等

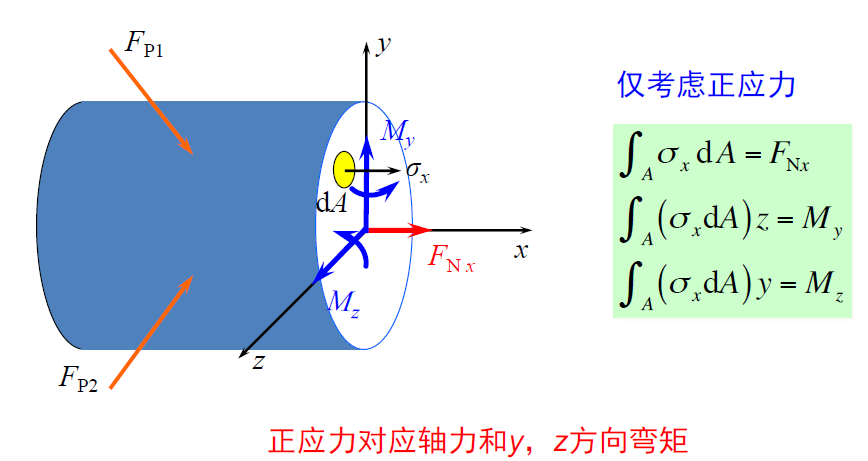
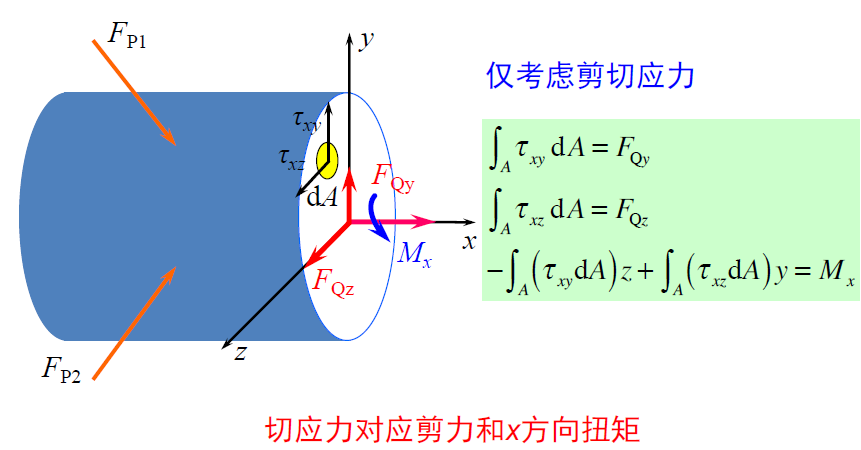
应力与内力

• 内力分量是截面上分布内力系(应力场)的简化结果。
• 因为应力是内力的集度，对于材料力学中研究的杆件系统， 应用积分方法，不难得到正应力与轴力、弯矩之间的关系式，剪应力与扭矩、剪力之间的关系式。

应力集中系数；这样我就可以通过算出平均正应力后，然后乘一个系数，就可以得到最大的正应力。

平均剪应力假定——后面学习知道是不合理的，理论与实验相结合

正应力与剪应变

• 如果将弹性体看作由许多微单元体所组成，这些微单元体简称微元体或微元(Element)。
• 弹性体整体的变形则是所有微元变形累加的结果。而微元的变形则与作用在其上的应力有关。
• 正应变——反应线的变形——注意泊松效应（体积发生了改变）；杆件中取出微元——不仅发生了伸长，也发生了平动，求梯度时该项消失——量纲为 1

$$
\epsilon_x = \frac{du}{dx}
$$

• 剪应变——在微元上建立剪应力，不考虑刚体转动——考虑直角的改变量

  • $\gamma=\alpha+\beta$
  • 与正应变有联系
  • 面积改变——基本不变

• 符号约定：

  • 拉应变为正；压应变为负。
  • 产生拉应变的应力(拉应力)为正；产生压应变的应力(压应力)为负。
  • 关于剪应力和剪应变的正负号将在以后介绍。

• 应变的大小与微元取向有关

• 应力与应变之间的关系：线弹性材料 Hooke 定律

• 泊松比$\nu$，杨氏模量 E 和剪切模量 G——知二求一

受力形式与材料力学性能

受力形式：

• 拉伸和压缩
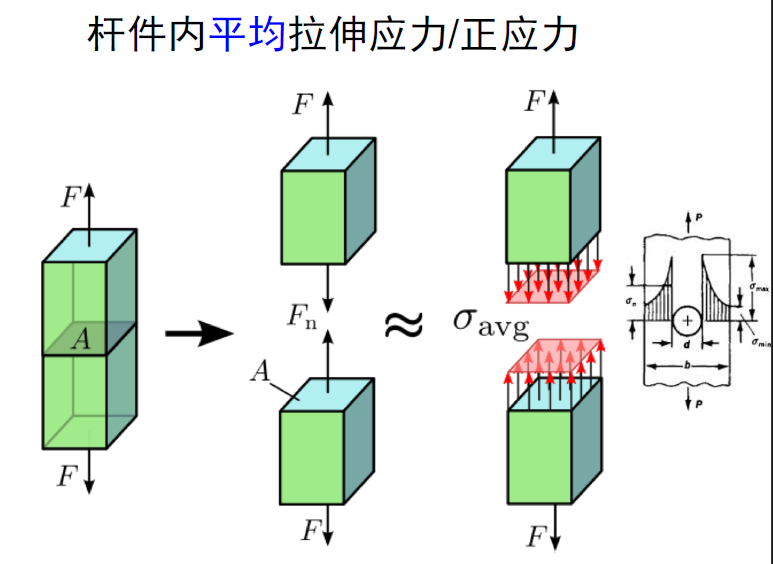
  • 当杆件两端承受沿轴线方向的拉力或压力载荷时，杆件将产生轴向伸长或压缩变形。
  • 距离段部远——可以认为均匀拉伸
  • 建立在平衡力系的基础上
• 剪切
  • 在平行于杆横截面的两个相距很近的平面内，方向相对地作用着 两个横向力，当这两个力相互错 动并保持二者之间的距离不变时，杆件将产生剪切变形 。
  • 剪切发生在局部——认为平均分布（应力）
• 扭转
  • 当作用在杆件上的力组成作用在垂直于杆轴平面内的力偶 Me时，杆件将产生扭转变形，即杆件的横截面绕其轴相互转动 。
  • 发生了剪切变形，如何衡量？
  • 在横截面上分析，单位长度半径转动角度——扭转角——线性剪应变分布
• 平面弯曲
  • 当外加力偶 M 杆件将发生弯曲变形，其轴线将变成曲线。
  • 利用线性叠加解决三维
  • 通过轴线变形表征弯曲程度
  • 界面上是线性分布的正应力
• 组合受力与变形
  • 小变形，线弹性（力与变形呈线性关系）

结论与讨论

• 关于弹性体受力与变形特点
  • 弹性体在载荷作用下，将产生连续分布的内力。弹性体内力应满足:
  • (1) 与外力的平衡关系；(外力与内力及应力之关系)
  • (2) 弹性体自身变形协调关系；(变形假设, 位移应变关系)
  • (3) 力与变形之间的物性关系。(Hooke 定律, 应力应变关系)杨氏模量与剪切模量
  • 这是弹性静力学与刚体静力学的重要区别。
• 关于工程静力学概念与原理在材料力学中的可用性与限制性
• 注意弹性体模型与刚体模型的区别与联系-刚体模型适用的概念、原理、方法，对弹性体可用性与限制性。诸如：力系的等效与简化；平衡原理与平衡方法等。
• 掌握逻辑：
  • 外力到内力——内力到应力——应力到应变——应变到变形
  • 三种方程：平衡方程；物理方程（Hooke 定律）；几何方程（变形假定，从杆件相对伸长——应力分布）——联系外部载荷和基本物理量的桥梁
  • 问题类型：强度、刚度、稳定性
  • 材料力学基本假定包括各向同性假定、均匀连续性假定。此外，为了分析的简化，还有小变形、线弹性等假定。
  • 不同于理论力学的地方（应变）