- 选择何种破坏?
- 相对大小进行讨论——何种失效
- 钢架结构——很多组件——组成钢架——固接——传递弯矩
- 直梁的弯矩;钢架的内力分析
剪力方程与弯矩方程
- 一般受力情形下,梁内剪力和弯矩将随横截面位置的改变而发生变化。描述梁的剪力和弯矩沿长度方向变化的代数方程,分别称为剪力方程 (Equation of Shear Force) 和弯矩方程(Equation of Bending Moment)。
- 为了建立剪力方程和弯矩方程,必须首先建立 Oxy 坐标系,其中 O 坐标原点,x 坐标轴与梁的轴线一致,坐标原点 y 一般取在梁的左端,x 坐标轴的正方向自左至右,y 坐标轴铅垂向上 (这会决定剪力、弯矩正方向的定义)。
- 建立剪力方程和弯矩方程时,需要根据梁上的外力(包括载荷和约束力)作用状况,确定控制面,从而确定要不要分段,以及分几段建立剪力方程和弯矩方程。
- 确定了分段之后,在每一段中任意取一横截面,假设这一横截面的坐标为 x,然后从这一横截面处将梁截开,并假设所截开的横截面上的剪力 FQ(x)和弯矩 M(x)都是正方向,最后分别应用力的平衡方程和力矩的平衡方程,即可得到剪力 FQ(x)和弯矩 M(x)的表达式,这就是所要求的剪力方程 FQ(x)和弯矩方程 M(x),即剪力与弯曲作为 x 函数的表达式。
例题 1:一端为固定铰链支座、另一端为辊轴支座的梁(简支梁)
- M 求导 FQ,FQ 求导——集度?
- 普遍吗?
- 后续讨论
例题 2:一道之前做过的题
- delta 函数描述间断点的求导——可以得到一个集中载荷的情况——妙不可言
载荷集度、剪力、弯矩之间的微分关系
作用在梁上的平面载荷,如果不包含纵向力,这时梁的横截面上将只有弯矩和剪力。表示剪力和弯矩沿梁轴线方向变化的图线,分别称为剪力图 (Diagram of Shear Force) 和弯矩图(Diagram of Bending Moment)。 绘制剪力图和弯矩图有两种方法:
(1)求解剪力方程和弯矩方程,在 FQ-x 和 M-x 坐标系中首先标出剪力方程和弯矩方程定义域两个端点的剪力值和弯矩值,并绘制出相应的图线,便得到所需要的剪力图与弯矩图;
(2)力和弯矩数值,然后应用载荷集度、剪力、弯矩之间的微分关系,确定控制面之间的剪力和
弯矩图线的形状,无需求解剪力方程和弯矩方程。
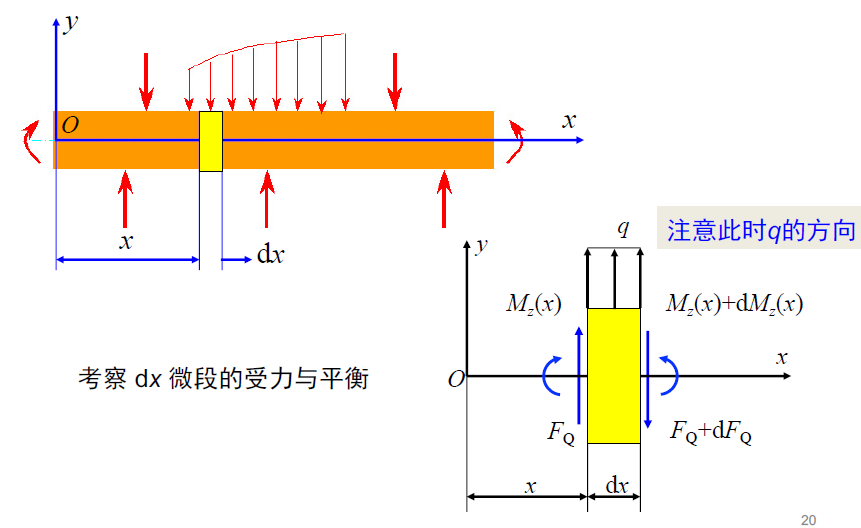
- 考察 dx 微段的受力与平衡
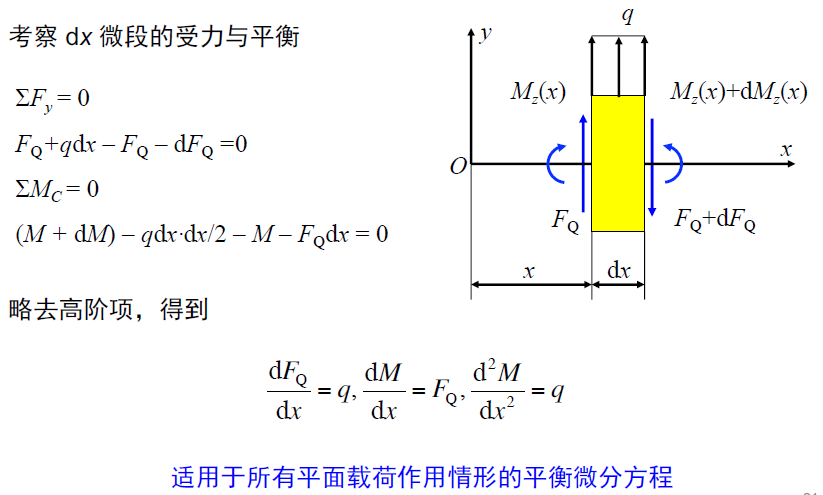
注意其中的方向定义!
• 剪力图的斜率等于作用在梁上的均布载荷集度;弯矩图在某一点处斜率等于对应截面处剪力的数值。
• 如果一段梁上没有分布载荷作用,即 q = 0,这一段梁上剪力的一阶导数等于零,弯矩的一阶导数等于常数,因此,这一段梁的剪力图为平行于 x 轴的水平直线;弯矩图为斜直线。
• 如果一段梁上作用有均布载荷,即 q = 常数,这一段梁上剪力的一阶导数等于常数,弯矩的一阶导数为 x 的线性函数,因此,这一段梁的剪力图为斜直线;弯矩图为二次抛物线。
• 弯矩图二次抛物线的凸凹性,与载荷集度 q 的正负有关: 当 q 为正(向上) 时,抛物线为凹曲线,凹的方向与 M 坐标正方向一致,当 q 为负(向下)时,抛物线为凸曲线,凸的方向与 M 坐标正方向一致。
剪力图与弯矩图

例题 3:间断点的作用规律
- AB 段与 CD 段的剪力相等,因而这两段内的弯矩图具有相同的斜率。
- 此外,在集中力作用点两侧截面上的剪力是不相等的,而在集中力偶作用处两侧截面上的弯矩是不相等的,其差值分别为集中力与集中力偶的数值,这是由于维持 DE 小段和 BC 小段梁的平衡所必需的。
例题 4:外伸梁(Overhanging Beam)
钢架的内力与内力图
- 刚架 (Rigid Frame) 或框架 (Frame)由两根或以上杆件通过刚性连接,包括横梁、立柱与刚节点。连接处夹角不变。
- 面内载荷作用下,刚架各杆横截面上的内力分量:轴力、剪力和弯矩。
内力图的画法
(1) 无需建立坐标系;
(2) 控制面、平衡微分方程;
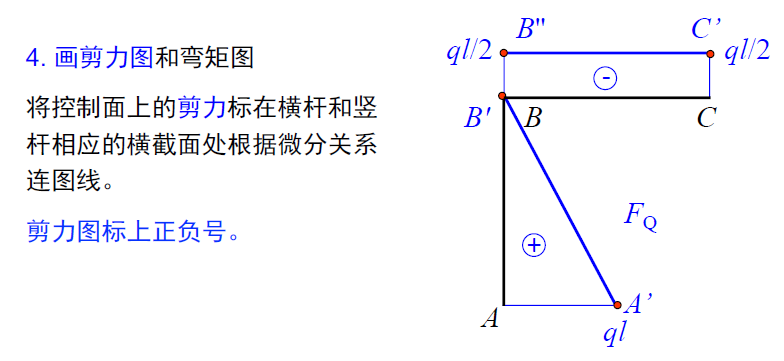
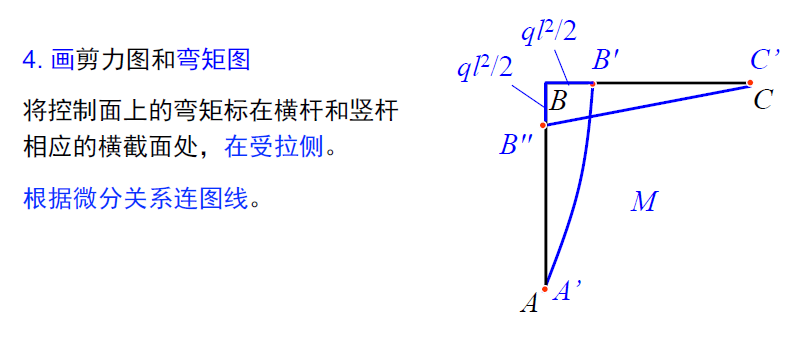
(3) 弯矩的数值标在受拉边;
(4) 轴力、剪力画在内侧和外侧均可,但需标出正负号;
(5) 注意节点处的平衡关系。
例题 5:画钢架内力图