写在前面
均匀变形与非均匀变形
- 比萨斜塔
- 桥式吊车
- 均匀分布载荷与集中载荷
- 如何描述梁的弯曲?
- 直线与曲线(挠度,转角)
- 反映塔
- 石油、化工设备
- 车轨——火车轮轴支撑在铁轨上
- 梁的弯曲
- 杆件承受垂直于其轴线的外力或位于其轴线所在平面内的力偶作用时,其轴线将弯曲成曲线。这种受力与变形形式称为弯曲。
- 主要承受由横向载荷或弯矩引起弯曲的细长杆件称为梁 (Beam)。
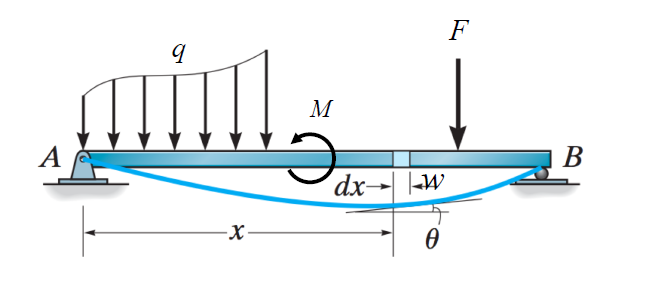
- 横向载荷和弯矩
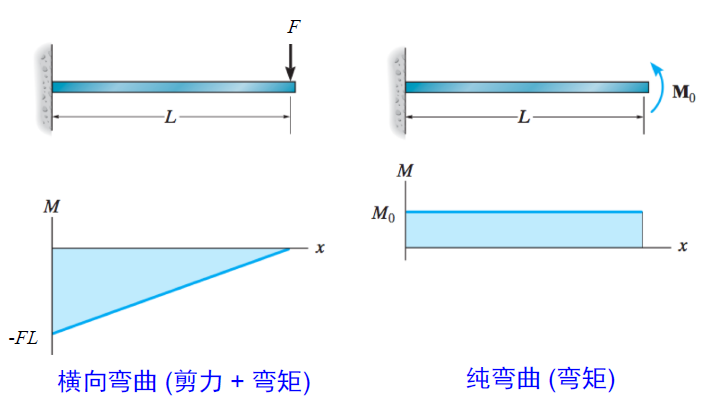
- 根据内力分析的结果,梁弯曲时,将在弯矩最大的横截面处发生失效。这种最容易发生失效的截面称为危险截面。但是,危险截面的哪一点最先发生失效? 怎样才能保证梁不发生失效?
- 这些就是本章所要讨论的梁强度问题。
- 纯弯曲是没有剪力的,我们最后再讨论这个问题
剪力和弯矩图
正负号约定
剪力、弯矩与载荷集度之间的微分关系
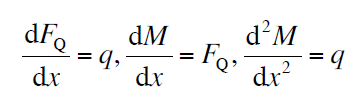
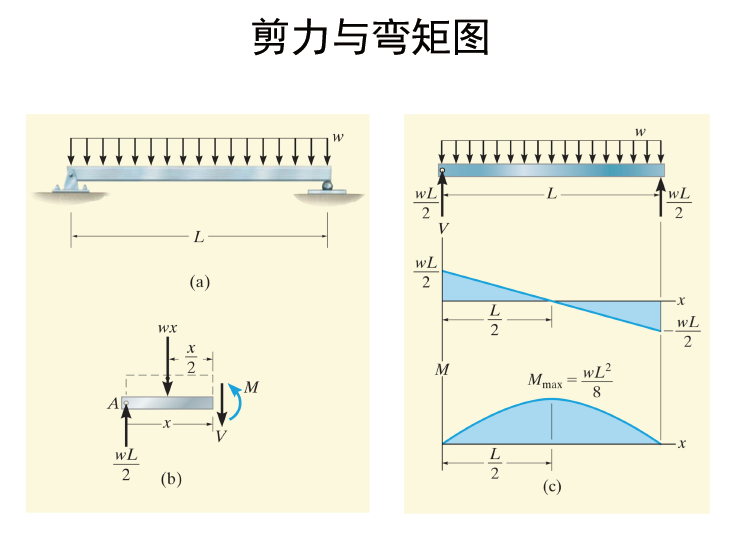
几种重要的梁的载荷图:
- 三点弯曲和四点弯曲
- 弯矩分布——方向一般指向下面,这样看上去比较好看
直梁弯曲的变形假定
平面弯曲问题
• 横截面存在一个形状对称轴
• 弯矩作用方向垂直与对称轴
- 问题就简化为平面弯曲——1 维问题+截面性质
- 对称轴(截面形状)——中性面(伸长、缩短分界)
- 中性面和轴线的交点就是截面的中心
- 如果用容易变形的材料,例如橡胶、海绵,制成梁的模型,然后让梁的模型产生纯弯曲,可以看到梁弯曲后,一些层发生伸长变形,另一些则发生缩短变形,在伸长层与缩短层的交界处那一层,称为梁的中性层或中性面(Neutral Plane)。中性层与梁的横截面的交线,称为截面的中性轴 (Neutral Axis)。中性轴垂直于加载方向,对于具有对称轴的横截面梁,中性轴垂直于横截面的对称轴。
注意:横截面也会有所变形!
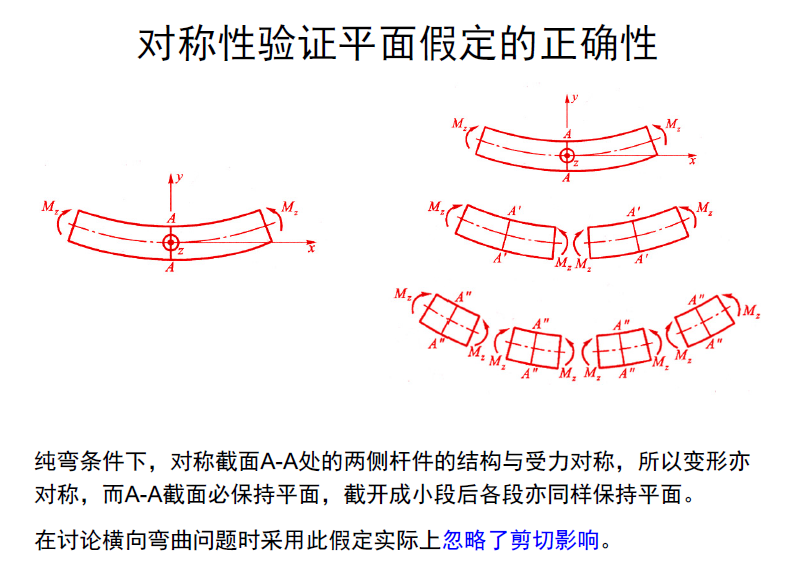
横截面保持平面 (平面假定)
纵向直线纤维 (局部) 变为圆弧 (纯弯曲,无剪切应力)——一个相当强的假定
横截面保持刚性,变形忽略不计 (不计泊松效应)类似与拉伸、压缩、剪切与扭转问题,用相邻的两个横截面从梁上截取长度 为 dx 的一微段,假定梁发生弯曲变形后,微段的两个横截面仍保持平面,但 是绕各自的中性轴转过一角度。这一假定称为平面假定 (Planar Assumption)。
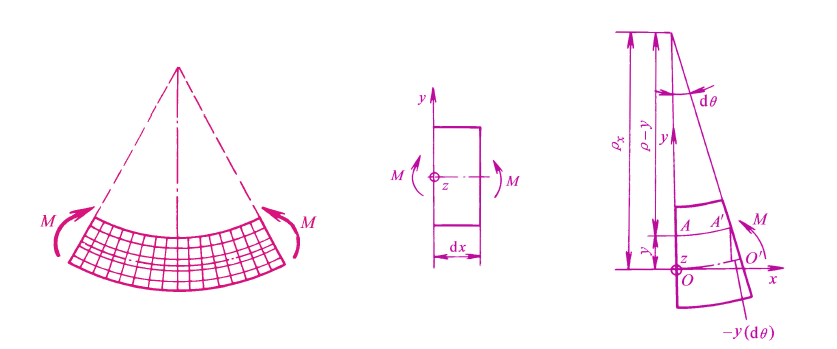

- 应用弹性范围内的应力应变关系的 Hooke 定律,得到正应力沿横截面高度分布的数学表达式
- 这表明,横截面上的弯曲正应力,沿横截面的高度方向从中性轴为零开始呈线性分布。
- 这一表达式虽然给出了横截面上的应力分布,
但仍然不能用于计算横截面上各点的正应力。
这是因为尚有两个问题没有解决:一是 y 坐标是从中性轴开始计算的,中性轴的位置还没有确定;二是中性面的曲率半径$\rho$也没有确定,
未与梁的侧向位移建立关系。
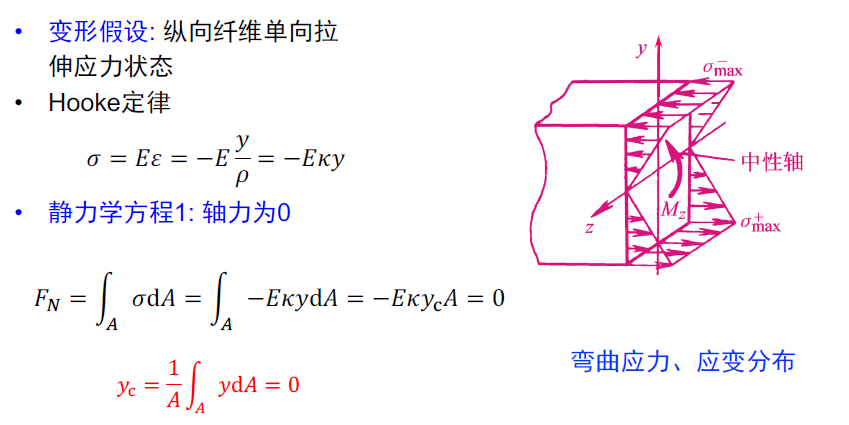
- 在纯弯条件下,当中性轴(坐标原点) 过形心时,yC = 0,轴力为零自动满足;当截面除弯矩外还存在轴力时,中性轴偏离形心位置。
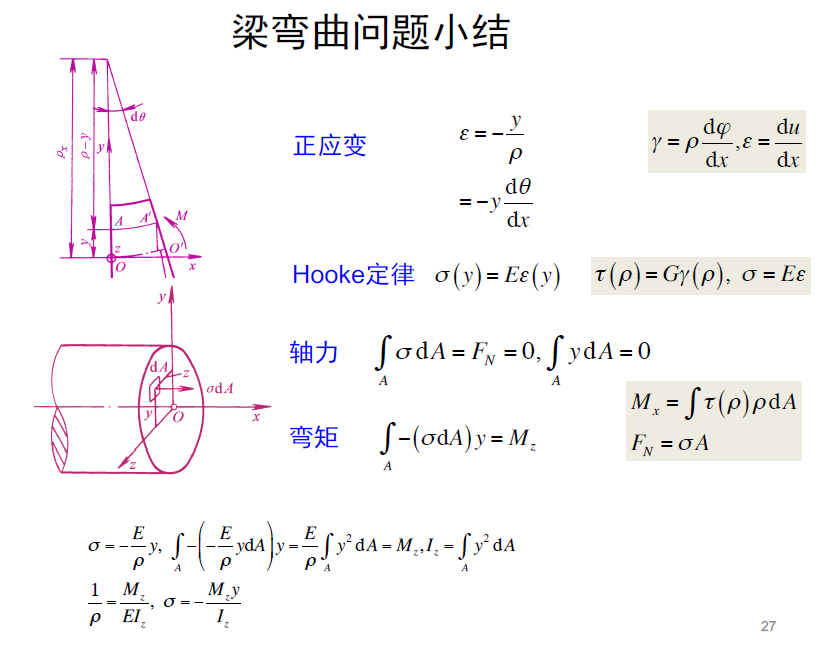
弯矩与曲率的关系

- I
z,载荷与弯矩之间的关系 - 理论框架:

截面的几何性质
静矩、形心及其相互关系
- 静矩——截面一次矩
- 静矩等于形心位置乘面积
- 静矩具有可加性,因此可以分解求复杂形体的形心
惯性矩、极惯性矩、惯性积、惯性半径
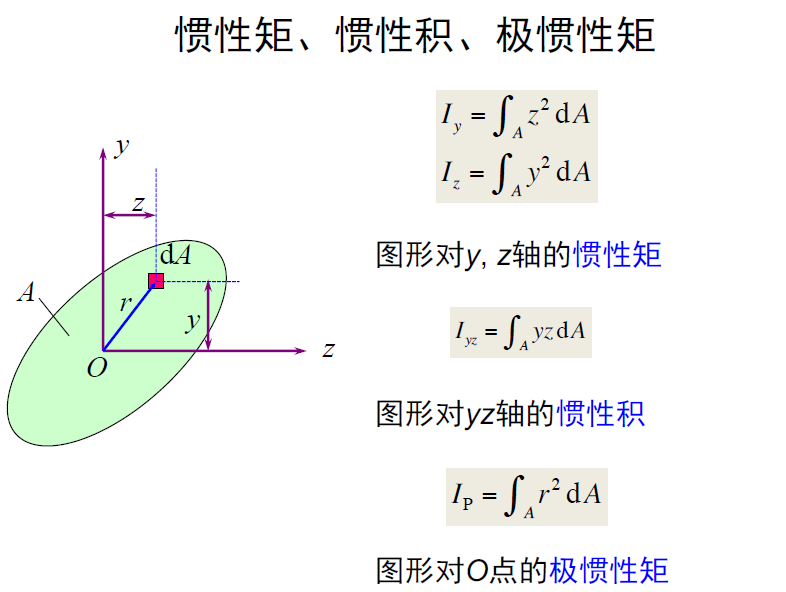
- 如果对称,那么惯性积等于零
- 惯性半径——可以算算
- 注意,只有在惯性积等于 0 时,才是平面弯曲
例题 1:圆柱
例题 2:矩形

惯性矩与惯性积的移轴定理
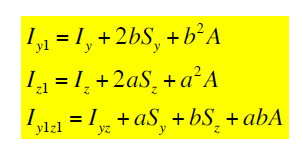
- 移轴定理

例题 3:求形心主矩
惯性矩与惯性积的转轴定理
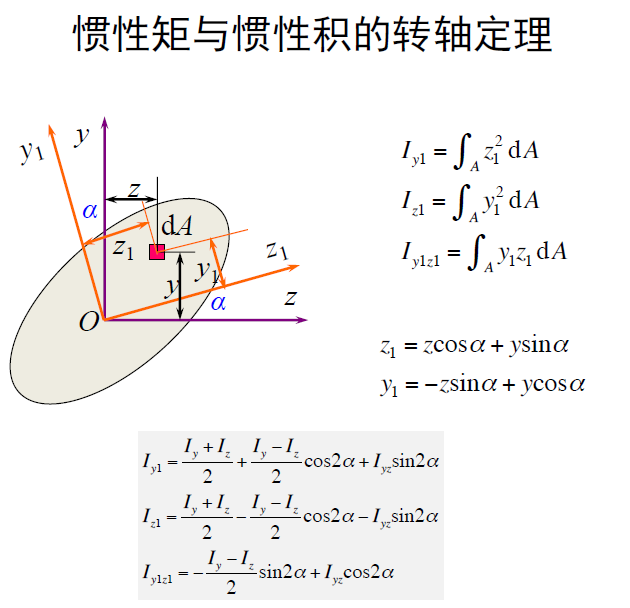
主轴与形心主轴、主惯性矩与形心主惯性矩
- 主轴——惯性积为 0
- 形心主轴——惯性积为 0,并且静矩等于 0
- 截面惯性矩使用矩阵表示
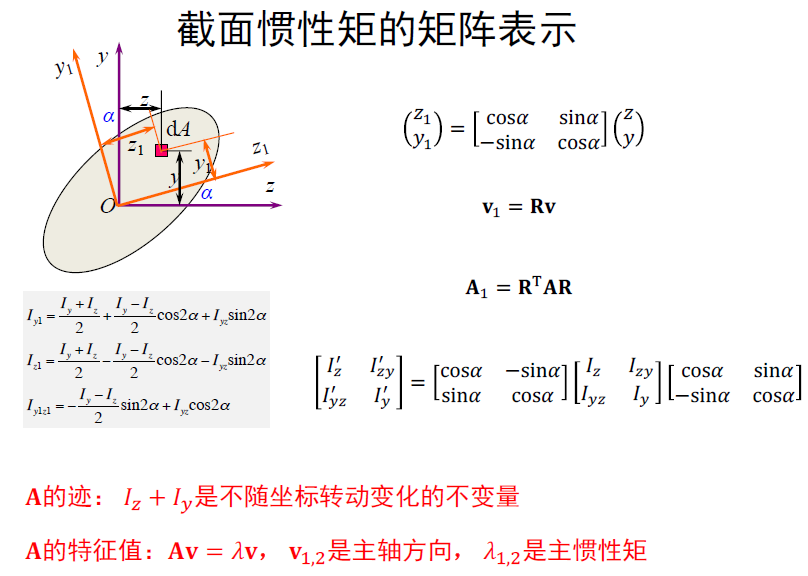
- 矩阵的迹——在转动中不变
- 特征方向与特征值
- 正多边形的截面惯性矩——无论什么方向,惯性积都为 0,都是它的主轴
- 做投影
弯曲正应力与强度设计

如何建立主轴?
中性轴的位置?
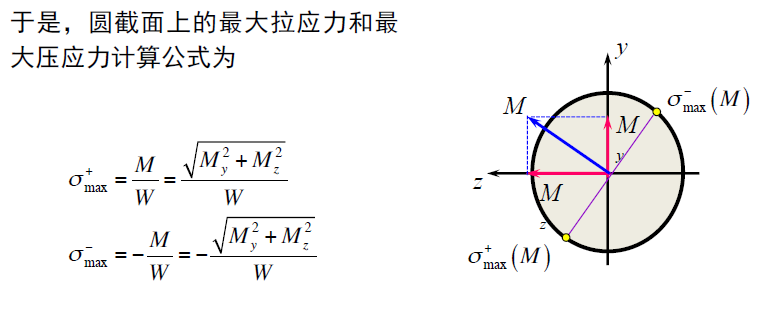
最大正应力的公式:

扭转截面系数;弯曲截面系数
例题 4:矩形截面梁
例题 5:简支梁,均匀分布载荷
例题 6:简支梁,集中力,T 形截面
梁强度失效判据
与拉伸或压缩杆件失效类似,对于韧性材料制成的梁,当梁的危险截面上的最大正应力达到材料的屈服应力 (σs) 时,便认为梁发生失效;对于脆性材料制成的梁,当梁的危险截面上的最大正应力达到材料的强度极限 (σb) 时,便认为梁发生失效。即
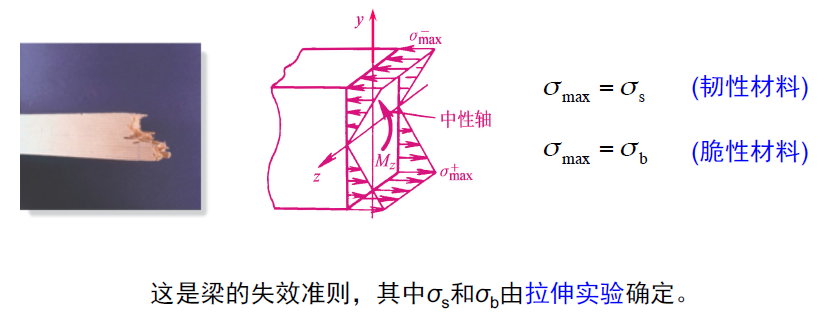
- 根据梁约束性质,分析梁的受力,确定约束力;
- 画出梁的弯矩图;根据弯矩图,确定可能的危险截面;
- 根据应力分布和材料的拉伸与压缩强度性能是否相等,确定可能的危险点:对于拉、压强度相同的材料 (如低碳钢等),最大拉应力作用点与最大压应力作用点具有相同的危险性,通常不加以区分;对于拉、压强度性能不同的材料 (如铸铁等脆性材料) 最大拉应力作用点和最大压应力作用点都有可能是危险点;
- 应用强度条件进行强度计算。
例题 7:圆轴,强度校核
例题 8:T 字形梁,拉伸、压缩许用力不同
例题 9:工字钢选用问题
斜弯曲与拉伸、弯曲组合
斜弯曲
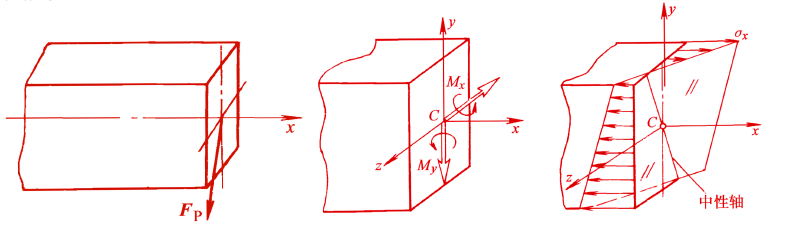
当外力施加在梁的对称面(或主轴平面)内时,梁将产生平面弯曲。所有外力都作用在同一平面内,但是这一平面不是对称面 (或主轴平面),梁也将会产生弯曲,但不是平面弯曲,这种弯曲称为斜弯曲 (Skew Bending)。
还有一种情形也会产生斜弯曲,这就是所有外力都作用对称面(或主轴平面)内,但不是同一对称面(梁的截面具有两个或两个以上对称轴) 或主轴平面内。
为了确定斜弯曲时梁横截面上的应力,在小变形条件下,可将斜弯曲分解成两个纵向对称面内 (或主轴平面) 的平面弯曲,然后将两个平面弯曲引起的同一点应力的代数值相加,便得到斜弯曲在该点的应力值。
以矩形截面为例,当梁的横截面上同时作用两个弯矩 My 和 Mz (二者分别都作用在梁的两个对称面内) 时,两个弯矩在同一点引起的正应力叠加后,得到总的应力分布图。
由于两个弯矩引起的最大拉应力发生在同一点;最大压应力也发生在同一点,因此,叠加后,横截面上的最大拉伸和压缩正应力必然发生在矩形截面的角点处。
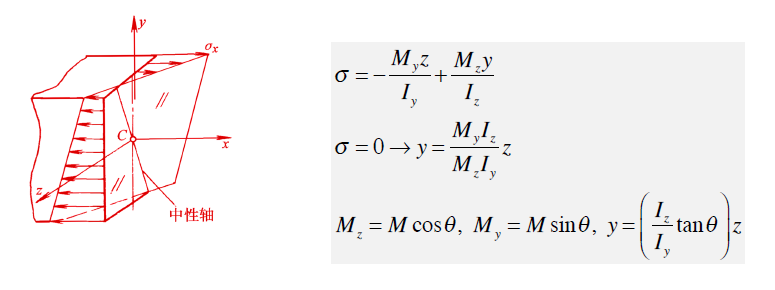
例题 10:校核梁的强度,斜弯曲
拉伸、弯曲组合
例题 11:校验立柱的强度,偏心加载
弯曲剪应力
纯弯曲和横向弯曲
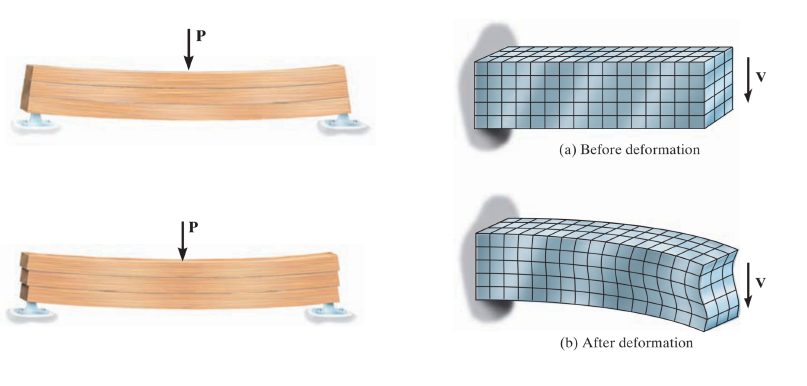
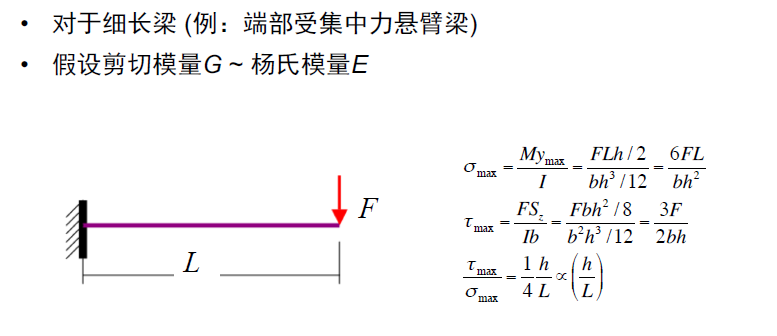
- 剪切效应对细长梁可以忽略不计
- 剪应力互等定理——上下轮廓无剪应力,左右轮廓沿轮廓方向
截面弯曲剪应力分布
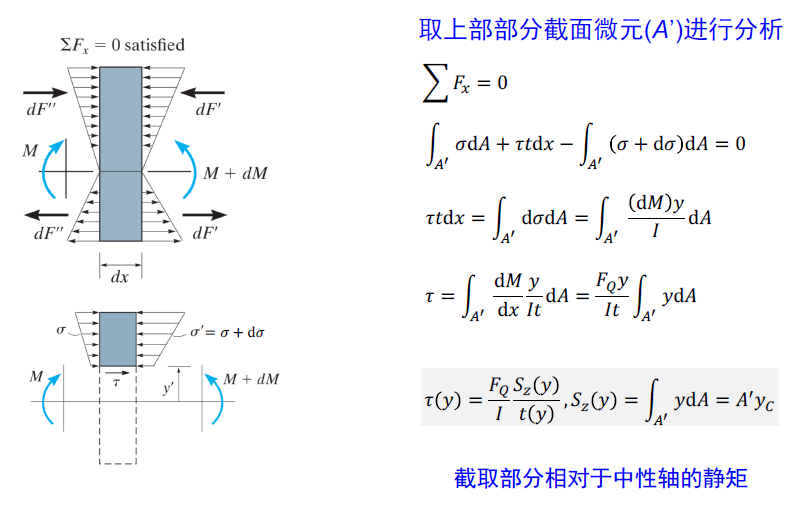
例题 1:矩形截面
例题 2:圆形、环形截面
- 注意适用范围!
- 宽度方向不均匀
- 宽度改变
- 工字梁——内壁剪应力
薄壁截面与剪应力流
例题 3:薄壁工字梁
基于弯曲剪应力的设计
- 连接件的强度设计
- 弯曲与剪切中心——主矢和主矩
细长杆件中的弯曲剪应力
- 可以通过公式计算
结论与讨论
应力分析与正应力公式
- 应力分析中,重要的是要确定应力分布规律,在此基础上即可由静力学平衡方程确定各点的应力表达式,要注意内力、应力的正负号约定。
弯曲刚度增强
- 选择合理的截面形状
- 采用变截面梁或者是等强度梁
- 改善受力状况
应力集中
- 小孔与倒角
非弹性弯曲
复合材料杆、梁横截面应力分布
- 使用截面等效法
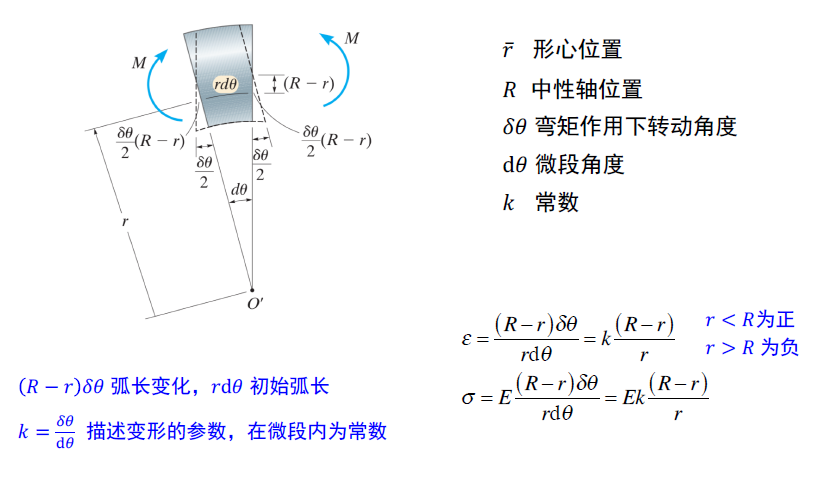
曲梁

小结











