从运动学的角度对有旋流动的流场作进一步的讨论和分析。
从动力学的角度介绍在质量力有势,流体为理想不可压缩的条件下,有关涡通量的保持性定理。
论述势流理论的基本内容,引出不可压缩流体平面流动的流函数概念,重点讨论不可压缩流体平面无旋流动的速度势函数与流函数的关系以及求解势流问题的奇点叠加方法。
有旋流动

有旋流动——旋度不为 0
涡量、涡线、涡管和涡通量
涡量:
对于有旋流动,将流速场的旋度称为涡量,它是流体微团旋转角速度矢量的两倍。涡量场是矢量场。
涡线:
涡线是涡量场的矢量线,是某瞬时对应的流场中的曲线,该瞬时位于涡线上各点对应的涡量都沿着涡线的切向。与流线一样,涡线是与欧拉观点相对应的概念。

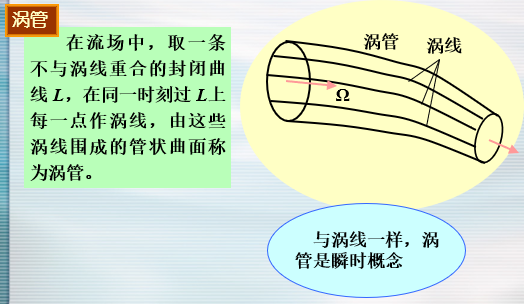
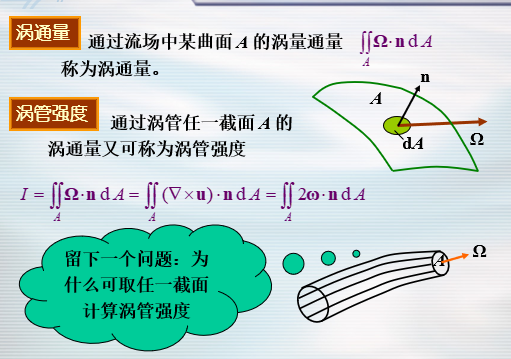
- 不可能有涡线穿入、穿出涡管
速度环量、斯托克斯定理
定义流速矢量 u 沿有向曲线 L 的线积分为速度环量
沿 L 的速度环量=通过 A 的涡通量
涡旋随空间的变化规律
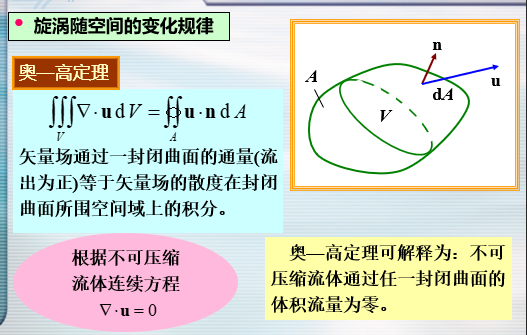
- 涡量场是无源场
- 涡管不能在流体中产生与消失,要么成环形,要么两端位于流场的自由面或固体边界。
漩涡随时间变化的规律
- 封闭流体线上的速度环量对于时间的变化率等于此封闭流体线上的加速度环量。
- 速度环量对时间的全导数等于加速度环量
无旋流动与有旋流动的等价性
开尔文定理

- 加速度有势——加速度无旋——加速度环量为 0(封闭流体线上)
- 封闭流体线上的速度环量不随时间变化——$\Gamma=const$
亥姆霍兹定理
- 某时刻组成涡管的流体质点将永远组成涡管。
- 涡管强度不变(在流动中)
- 容易通过开尔文定理予以证明,上述亥姆霍兹定理成立的条件应与开尔文定理相同。
粘性对旋涡运动的影响
- 开尔文定理说明,若质量力有势,流体为理想不可压缩流体,那么涡通量不会产生,初始时刻为无旋的流动将永远保持无旋,而有旋流动的涡通量则有保持性,既不会消失,也不会扩散。
- 开尔文定理也反过来说明了之所以在实际流体的运动中会有旋涡的产生、发展和消失,以及涡量在流场中的扩散现象,
粘性 的存在应该是最重要的因素。
诱导流速、兰肯涡和卡门涡街
兰肯涡
- 平面组合涡:中心区是强迫涡;外围区是自由涡
- 中心区是以涡心为圆心的圆,其中的速度与离涡心的距离成正比,涡量为常数。外围部分的流速则与离涡心的距离成反比,流动有势,涡量为零。
- 兰肯涡是比较接近实际的平面旋涡模型,其中心部分的流体象刚体一样旋转,需有外力不断推动,中心部分也可用圆柱形刚体的转动来代替。外围部分流体的运动在开始时是由中心部分的转动通过粘性的作用形成的,在流动稳定以后,则无须再加入能量,粘性也就不再起作用。
- 中心区——涡量处处为常数
- 外围区是无旋流动
- 故外围区可通过欧拉积分确定压强的径向分布
- 中心区只能用伯努利积分,但得不到压强的径向分布,所以直接使用理想流体的运动方程
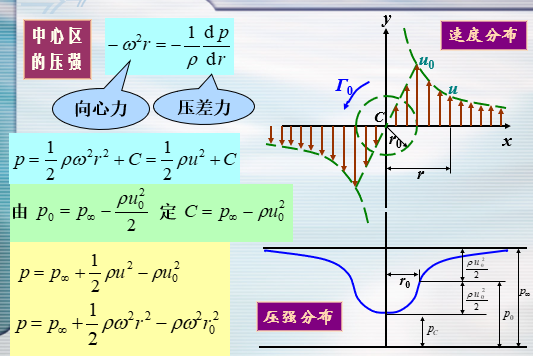
- 下方的为抛物线——故有一个焦点
- 抛物线分布,涡心处最低
- 中心区速度越快,压强越高,速度越慢,压强越低。与无旋区有本质的不同。
卡门涡街
- 试验发现,定常来流 U 绕过直径为 d 的圆柱体时,在不同雷诺数情况下,圆柱下游有不同的旋涡现象出现。当雷诺数大于 90 后,可以看到有规则交错排列的双列线涡,称为卡门涡街,其中尤以雷诺数等于 150 左右时最为典型。

- 从柱体上、下面分别脱落的旋涡,其旋转方向是彼此相反的,同时所有旋涡都以相同速度(因有旋涡间相互干扰,此速度比来流速度小)向下游移动。
有势流动及解法概述
由开尔文定理可知,理想不可压缩流体从静止或无旋状态开始的流动将保持为无旋流动。所以无旋流动往往是以理想流体为前提条件的。无旋流动即为有势流动。
无旋流动有速度势函数

极坐标系中速度势函数的微分:
- 不可压缩流体无旋流动的速度势函数满足拉普拉斯方程
- 满足拉普拉斯方程的函数称为调和函数
$$
\nabla^2\phi = \Delta \phi=0
$$
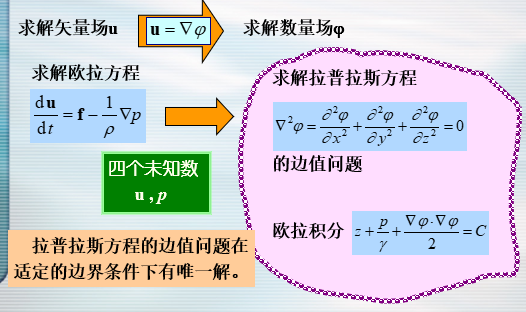
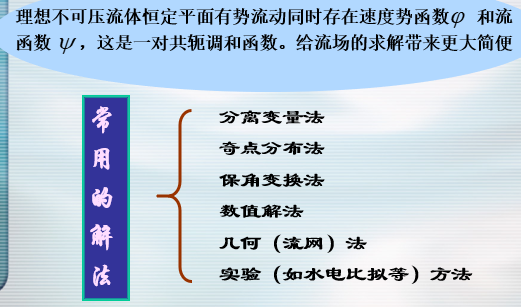
理想不可压缩流体恒定有势流动的解法概述
不可压缩流体平面流动的流函数
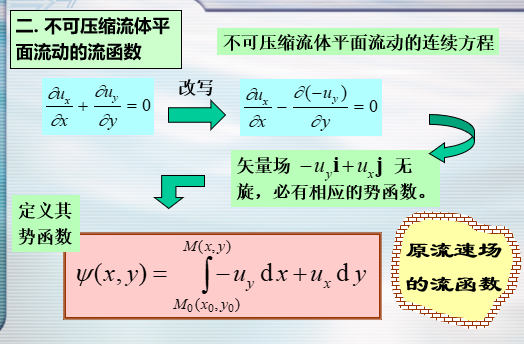
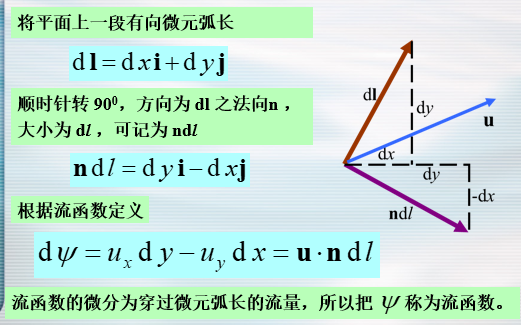
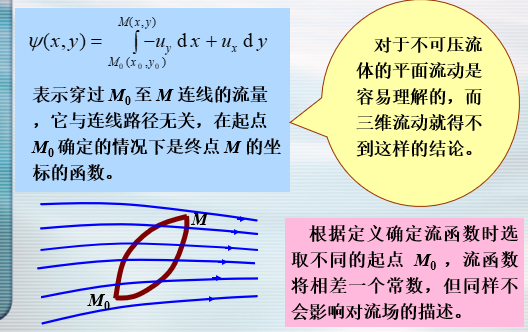
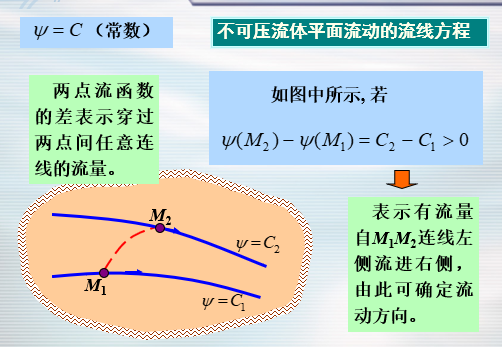
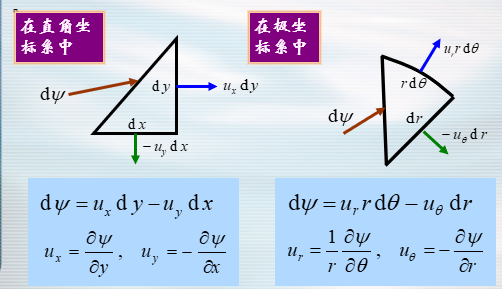
- 流函数也是调和函数——满足拉普拉斯方程
- 不可压流体平面无旋流动既有速度势函数又有流函数,它们都满足拉普拉斯方程,都是调和函数。
- 称这对调和函数满足柯西 — 黎曼条件,互为共轭调和函数。
- 等势线与等流函数线是相互正交的
- 以上速度势函数和流函数的关系是在不可压缩流体平面无旋流动的条件下建立的。
- 在不可压缩流体平面有旋流动中就只有流函数,没有速度势。
- 在不可压缩流体三维无旋流动中就只有速度势,没有流函数。
- 复势、复速度

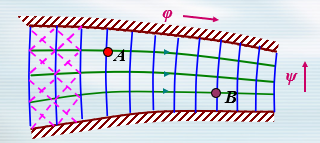
- 绘制流网是求解理想不可压流体定常平面有势流动的一种近似的几何方法,流网是由等速度势函数线族和等流函数线(流线)族构成的正交网格。一般取速度势函数和流函数的增量相等,流网呈正方形。根据流网可以图解流速,再由欧拉积分推算压力。
- **绘制流网要点:**固壁为等流函数线(流线);流线间隔按流量相同划分,断面流速均匀,则流线间距相等;自由面也是一条流线,但其位置、形状未知,需利用压强条件逐渐确定。
- 流网密处,流速大、压强小。流网疏处,流速小、压强大。已知一点处流速、压强,可知各点流速和压强。
理想不可压缩流体恒定平面势流的奇点分布解法
几种基本的不可压缩流体平面有势流动
- 直线等速流动
- 平面点源
- 平面点涡
- 平面偶极子=点源+点汇
基本有势流动的叠加
将零流线认为是壁面
设想用一刚性薄片按上述过驻点流线的形状弯成柱面,从垂直于流动平面的方向插入流场,将不会影响内外两部分流场的流动。这就是流线与固壁的等价原理。若按过驻点流线的形状制成半无穷柱体放入流场相应位置,取代点源,此时内部流动将不再存在,但外部流动仍不会改变。所以点源对等速直线流动的影响与这个半无穷柱体对等速直线流动的影响是等价的。上面我们得到的流场也就是等速直线流动绕过半无穷柱体的绕流解。从这个意义上讲,点源这个抽象的流动变成了一个具体、实在的概念。
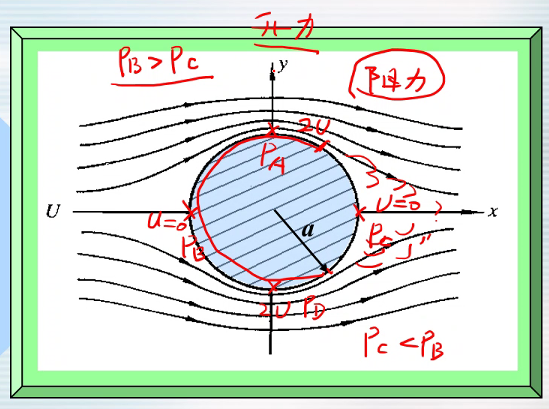
- 平行于流速方向——阻力
- 垂直与流速方向——升力
- 马格努斯力——在无环量圆柱绕流解的基础上再叠加一个绕圆柱的环量,即在原点加上一个平面点涡,易知圆柱面仍是流线,形成有环量的圆柱绕流。此时,圆柱面上的速度大小和压强分布不再是上下对称的了,因此引起升力。
- 升力产生——来流不均匀、形状不均匀、自转
- 阻力产生——压差阻力、……
- 流线——壁面
平面壁镜像法
过于奇葩










