- 流体静力学研究流体在静止状态下的受力平衡规律,由平衡条件求静压强分布,并求静水总压力。
- 静止是相对于坐标系而言的,不论相对于惯性系或非惯性系静止的情况,流体质点之间没有相对运动,这意味着粘性将不起作用,所以流体静力学的讨论不需区分流体是实际流体或理想流体。
流体静压强的特性
- 流体静压强的方向沿作用面的内法线方向
- 静止流体质点间的相互作用以压应力形式体现,压应力即为静压强。静压强只能是垂直并指向作用面,即静压力只能是垂直的压力(流体质点之间没有相对运动不存在切应力)。
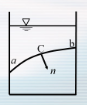
- 静止流体中任一点上流体静压强的大小和作用面的方位无关,即同一点上各个方向的流体静压强大小相等
- 简要证明:利用流体微元(取四面体状流体微元)
- $\displaystyle p_ydA_y-p_ndA_ncos(n, y)+\rho YdV=0$
- $Y$是质量力在y方向的分量
- $p_n=p_x=p_y=p_n$
流体平衡微分方程
平衡微分方程的推导
- 取微元体(六面体)分析y方向受力
- 表面力$\displaystyle pdxdz-(p+\frac{\partial p}{\partial y}dy)dxdz=-\frac{\partial p}{\partial y}dxdydz$
- 最终由质量力与表面力平衡,平衡方程为$\displaystyle\rho Y - \frac{\partial p}{\partial y}=0,\cdots$
- $\displaystyle f-\frac{1}{\rho}\nabla p=0$
- $\nabla p$的三个分量是压强在三个坐标轴方向的方向导数,它反映了数量场在空间上的不均匀性
- 反映了质量力和压差力之间的平衡,压强对流体受力影响是通过压差来体现的
静压强的分布规律
重力场中液体静压强的分布
- 重力作用下的平衡方程
- $f = -gk$, $\displaystyle \frac{dp}{dz}=-\rho g=-\gamma$
- $\gamma$被称为重度,因此$p=-\gamma z+C$或$\displaystyle z+\frac{p}{\gamma}=C$
- 自由面作为基准面 z=0,自由面上压强为 p
0,则$p=p_0-\gamma z$ - 水深 h=-z,那么就可以表示为$p=p_0+\gamma h$
- 在重力作用下的静止流体中,压强随深度按线性规律变化。
- 等压面——在重力作用下的静止流体中具有相同的静压强值的面
- 只有重力作用下的等压面应满足的条件:
- 静止;连通;连通的介质为同一均质流体
- 量力仅有重力;同一水平面
- 绝对压强、相对压强、真空
- 绝对压强——以完全真空为零点,记为 p
abs - 相对压强——以当地大气压 p
a为零点,记为 pr - 真空压强——相对压强为负值时,其绝对值称为真空压强。
- 默认为相对压强$p$,若指绝对压强则特别注明
- 绝对压强——以完全真空为零点,记为 p
- 水头与单位势能
- 将水柱高称为
水头 - 把真空压强转换成水柱高表示,称为
真空度 。 - 位置水头——z,铅锤面竖直向上
- 压强水头——$\displaystyle \frac{p}{\gamma}$
- 测管水头(测压管水头)——$\displaystyle z + \frac{p}{\gamma}$
- 测静压只须一根测压管
- 长度单位——可以认为是单位重量液体的能量
- z——代表了单位重量流体所具有的位能
- $\displaystyle \frac{p}{\gamma}$代表了单位重量流体所具有的压能
- 液体平衡规律表明:位置水头(势能)与压强水头(势能)可以互相转换,但它们之和 —测压管水头(总势能)是保持不变的。
- 流体的平衡规律必须在连通的静止流体区域(如测压管中)应用,不能用到管道中去,因为管道中的流体可能是在流动的,测压管不只是为测量静压用的。
- 将水柱高称为
静止液体作用在物体表面上的总压力
作用在平面上的液体总压力
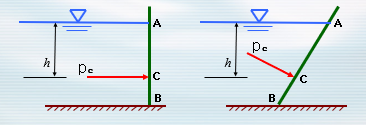
- 水力自动翻转闸门
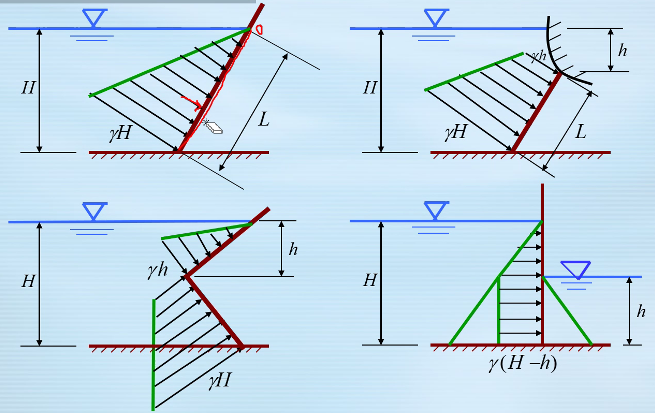
- 作用于平面的静水压力=压强分布图形的体积,并通过该体积的重心。
- 任意形状平面上静水总压力——平面的平均压强与形心压强相等
- 总压力的作用点:
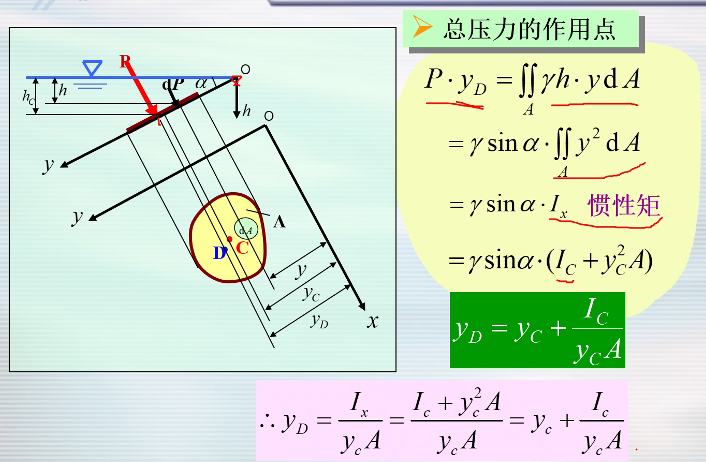
- 1.平面上静水压强的平均值为作用面(平面图形)形心处的压强。总压力大小等于作用面形心 C 处的压强 p
C乘上作用面的面积 A . - 2.平面上均匀分布力的合力作用点将是其形心,而静压强分布是不均匀的,浸没在液面下越深处压强越大,所以总压力作用点位于作用面形心以下。
作用在曲面上的液体总压力
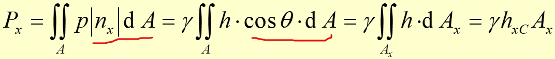
- 静止液体作用在曲面上的总压力在 x 方向分量的大小等于作用在曲面沿 x 轴方向的投影面上的总压力。
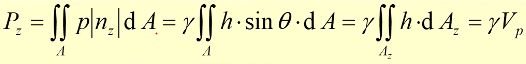
- 静止液体作用在曲面上的总压力的垂向分量的大小等于压力体中装满此种液体的重量。
- 总压力垂向分量的方向根据情况判断。
- 复杂柱面的压力体
分层流体 情况时,显得尤为重要
阿基米德定律
- 静止液体作用在物体上总压力—浮力的大小等于物体所排开液体的重量,方向铅垂向上,作用线通过物体被液体浸没部分体积的形心—
浮心 。
为什么竖直方向作用点、水平方向作用点、实际作用点不是同一个点
- 可以用少一块来想
- 这样 x 方向受力不变、但是总体受力发生了变化
- 所以得到不是同一个点
流体的相对平衡
- $\displaystyle f-\frac{1}{\rho}\nabla p=0$变为$\displaystyle f-a-\frac{1}{\rho}\nabla p=0$
- 表面力中仍无切应力
- 根据此种方法,可以做出加速度计
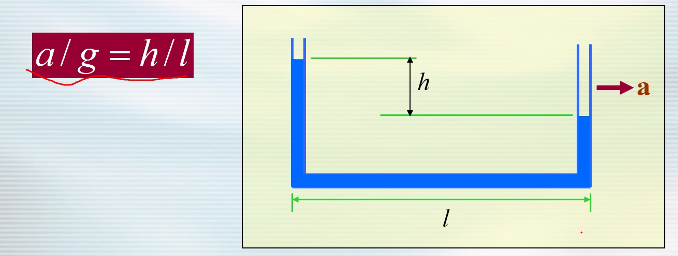
- 这就是第二讲










