流体运动学

描述流动运动的方法

• 在连续介质假设下，讨论描述流体运动的方法，根据运动要素的特性对流动进行分类
• 本章讨论是纯运动学意义上的，不涉及流动的动力学因素，对理想流体和粘性流体均适用
• 流体相对于固体来说还是较为复杂的
• 无穷多个质点，还有自由度
• 拉格朗日描述、欧拉描述
• 拉格朗日法——质点系法——**研究单个流体质点的运动全过程，记录它们在运动过程中位移的时间历程，通过综合所有质点的运动，构成整个流体的运动。**
• 特点：
  • 在概念上简明易懂，和研究固体质点运动的方法极其相似；
  • 跟踪流体质点的过程中，时间和质点所处空间位置会同时变化，带来数学处理上的困难；
  • 从实用的观点来看，常常并不需要知道每个个别质点的运动细节，这种方法在水力学上很少采用。
• 欧拉法Eular——流场法

• 把着眼点放在空间点，观察先后流经这一空间点的各个流体质点的运动情况。综合所有的空间点的情况，构成整个流体的运动。
• 欧拉法把流场的运动要素和物理量都用场的形式表达，为在分析流体力学问题时直接运用场论的数学知识创造了便利条件。
• 欧拉法——常用方法
• 但是——求解加速度？
  • 通过位移求速度或通过速度求加速度，必须跟定流体质点，应该在拉格朗日观点下进行。
  • 若流场是用欧拉法描述的，流体质点加速度的求法必须特别注意。
  • $\displaystyle \frac{du}{dt}=\frac{\partial u}{\partial t} + (u·\nabla)u$
  • 方程左侧为质点加速度，右侧为时变加速度+位变加速度，即：
  • 固定空间点，由时间变化引起的加速度，同一时刻，由流场的空间位置变化引起的加速度
  • 本质上来讲就是加了一项，又减了一项

有关流场的几个基本概念

恒定流、非恒定流

• 看时变加速度——恒定流的时变加速度为零，但位变加速度可以不为零。
• 若流场中各空间点上的任何运动要素均不随时间变化，称流动为恒定流。否则，为非恒定流。
• 恒定流中，所有物理量的欧拉表达式中将不显含时间，它们只是空间位置坐标的函数，时变导数为零。

迹线与流线

• 迹线 (Path line)：同一质点在各不同时刻所占有的空间位置连成的空间曲线称为迹线。
• 流线：同一时刻，不同质点运动的切线方向的连线。在某一时刻，各点的切线方向与通过该点的流速方向重合的空间曲线称为流线。

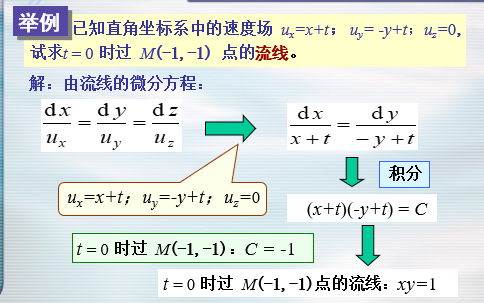
• 根据流线的定义，可以推断：除非流速为零或无穷大处，流线不能相交，也不能转折。
• 在非恒定流情况下，流线一般会随时间变化。在恒定流情况下，流线不随时间变，流体质点将沿着流线走，迹线与流线重合。
• 迹线和流线最基本的差别是：迹线是同一流体质点在不同时刻的位移曲线，与拉格朗日观点对应，而流线是同一时刻、不同流体质点速度矢量与之相切的曲线，与欧拉观点相对应。即使是在恒定流中，迹线与流线重合，两者仍是完全不同的概念。

流管和流量

• 在流场中，取一条不与流线重合的封闭曲线 L，在同一时刻过 L 上每一点作流线，由这些流线围成的管状曲面称为流管。
• 与流线一样，流管是瞬时概念。
• 根据流管的定义易知，在对应瞬时流体不可能通过流管表面流出或流入。
• 过流断面——**与流动方向正交的流管的横断面**
• 流量：体积流量 Q：单位时间通过过流断面的流体体积
• 元流流量：

均匀流与非均匀流

• 位变导数=0
• 应注意将均匀流与完全不随空间位置而变的等速直线流动相区别，前者是流动沿着流线方向不变，后者是流动沿着空间任何方向不变。后者是均匀流的一个特例。

维数分类

• 一维流动
• 二维流动
• 三维流动

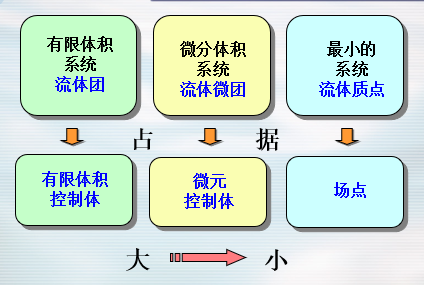
系统和控制体

• 由确定的流体质点组成的集合称为系统。系统在运动过程中，其空间位置、体积、形状都会随时间变化，但与外界无质量交换。
• 有流体流过的固定不变的空间区域称为控制体，其边界叫控制面。不同的时间控制体将被不同的系统所占据。
• 站在系统的角度观察和描述流体的运动及物理量的变化是拉格朗日方法的特征，而站在控制体的角度观察和描述流体的运动及物理量的变化是欧拉方法的特征。

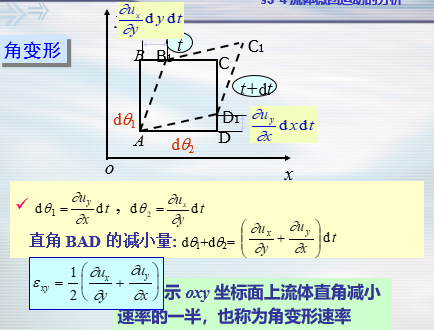
连续微团运动的分析

• 考察和分析流体质点之间的相对位移和相对运动
• 谈及相对运动就必须把讨论问题的尺度从流体质点扩大到流体微团
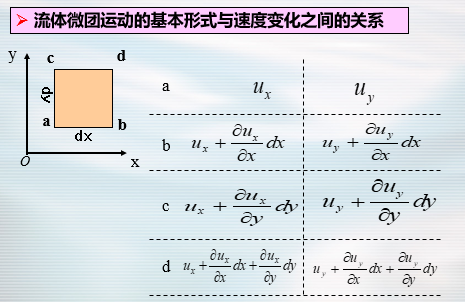
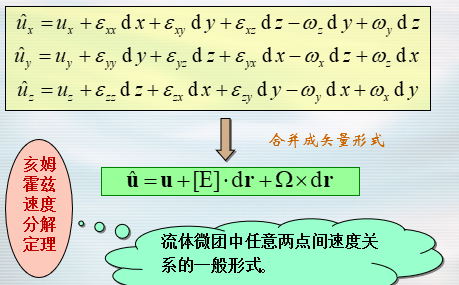
• 给出在同一时刻流体微团中任意两点速度之间的关系。
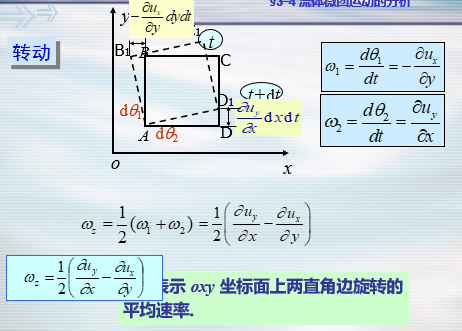
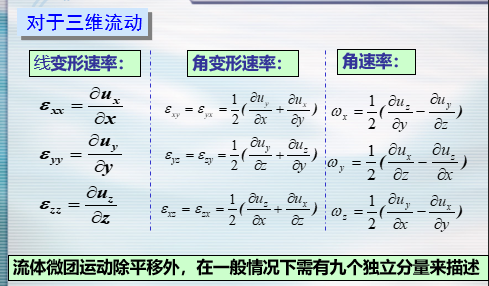
• 分析流体微团的运动形式
• 微团运动的基本形式：平移、转动和变形

• 亥姆霍兹速度分解定理

• 有旋流动和无旋流动

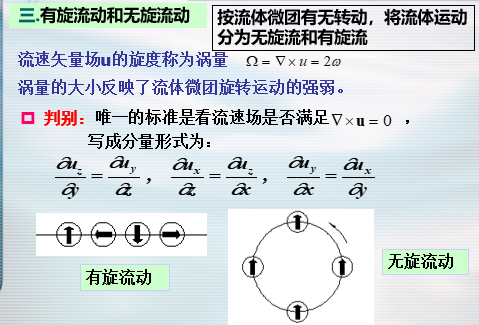
• 无旋流动又等价于有势流动

连续性方程

• 连续性方程 —— 各种流动都必须遵循的一个基本方程。质量守恒定律对流体运动的一个基本约束。

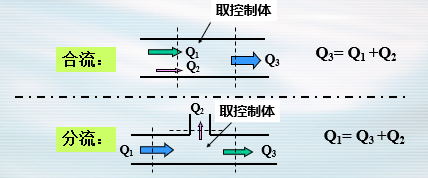
• 控制体：上游过流断面 A1 和下游过流断面 A2 之间的总流管

• 恒定条件下：

  • 总流管的形状、位置不随时间变化。
  • 总流内的流体是不存在空隙的连续介质，其密度分布恒定，所以这段总流管内的流体质量也不随时间变化。
  • 没有流体穿过总流管侧壁流入或流出，流体只能通过两个过流断面进出控制体。

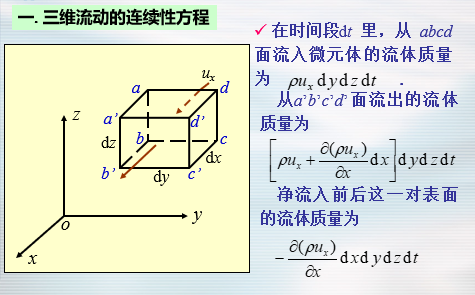
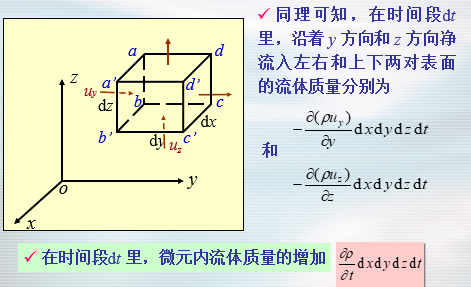
• 用欧拉观点对质量守恒原理的描述：
• 连续介质的运动必须维持质点的连续性，即质点间不能发生空隙。因此，净流入控制体的流体质量必等于控制体内因流体密度变化而增加的质量。

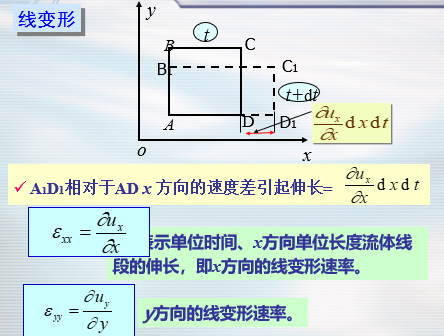
• 注：流体微团在三个互相垂直方向上的线变形速率之和，也是流体微团的体积膨胀率。
• 连续方程$\nabla ·u=0$表明不可压缩流体微团在三个互相垂直方向上的线变形速率的总和必为零，若在一个方向上有拉伸，则必有另一个方向上的压缩，在运动过程中其体积不会发生变化。
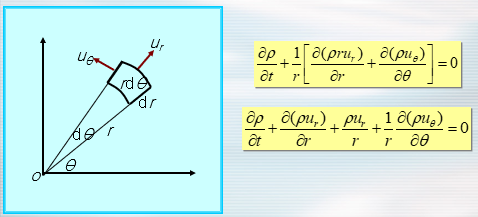
• 如果是极坐标？

小结

• 了解描述流体运动的两种方法。

• 正确理解欧拉法、质点加速度、质点导数、流线等物理意义，并能在直角坐标系下进行计算。

• 了解流体微团的基本形式，正确区分和判别恒定流与非恒定流，均匀流与非均匀流，有旋流动和无旋流动。

• 正确理解连续性方程的物理意义。