绪论 - Xiao Space

病毒传播的流体力学原理

勤洗手、多通风、戴口罩
流感病毒 0.1$\mu m$
咳嗽时，飞沫可以传播 6m 左右
咳嗽和喷嚏的飞沫会在1~2m之内掉落到地面，只有较小的水滴会以气溶胶形式停留在空中
咳嗽飞沫6m，保持悬浮，最多可悬浮10min
喷嚏——形成湍流——最多漂移8m

绪论

流体运动与流体力学

空气、水等都是流体，虽然人生活在流体环境中，人们对流体运动现象却缺乏认识。

飞机

机翼升力来自于上部还是来自于下部？
- 人们直观印象是空气从下面冲击鸟的翅膀，
- 机绕流
足球，香蕉球与电梯球
- 物体转动，马格努斯效应
- 物体高速运动——粗糙区、光滑区

流体力学的概念、研究方法与应用

概念：研究流体的平衡和流体机械运动规律及其实际应用的技术科学
应用：气象、水文、水利、环保、农业、航空、航海、渔业、国防等等部门研究的对象；人工智能，机器人也有涉及，在许多设备中工作介质也是流体
课程地位：重要的专业基础课，连接前期基础课程和后续专业课的桥梁
研究方法：理论分析，实验研究和数值计算（计算流体力学 CSB）相结合。三方面互相补充和验证，但又不能相互取代的关系
数值模拟——需要证明结果正确性
水力学的应用：核电站——排水分层
中华鲟相关问题
- 回游型鱼类——在海里生活——回长江上游产卵——修建葛洲坝后——在葛洲坝下面产卵下降到 18 度以后开始产卵
- 由于水库水温的温值效应，所以产生了很大的影响——产卵时间发生变化（三峡之前 9、10 月，三峡之后 11 月）2013、2014、2015，没有发现中华鲟产卵情况。

流体的主要物理性质

流体的基本特性——流动性

流体在静止时不能承受剪切力以抵抗剪切变形，只有在运动状态下，当流体质点之间有相对运动，才能抵抗剪切变形
流体质点概念、连续介质假设
- 微观角度：流体由分子组成，分子之间存在间隙，在空间和时间上不连续
- 流体质点：宏观上足够小、微观上足够大，是宏观研究流体的最小单元
- 宏观角度：流体是由无数流体质点组成的，质点之间没有孔隙，连续地充满流体所占的空间
- 从统计角度看，趋于稳定
连续介质假设
- 定义：连续介质：质点连续充满所占空间的流体、固体；连续介质模型把流体视为没有间隙的充满它所占据的整个空间的一种连续介质
- 优点：排除了分子运动的复杂性；时空连续性，可以利用函数这一数学工具来研究问题；在很多情况下都成立，但是稀薄的空气不能作为连续介质处理；虽然不研究流体微观的分子运动，但是分子运动客观存在；所以必须考虑（例如粘性）
流体的主要物理特性——粘滞性
- 粘性：流体在运动时，具有抵抗剪切变形能力的性质。
- 粘性——>流速梯度（相对运动）——>近似直线运动，层层之间出现了反抗相对运动的内摩擦力 T
- 流体运动才有粘性还是流体相对运动才有粘性力？
- A——接触面（对具体问题不好确定）
- $$
  T=\mu A\frac{du}{dy}\qquad[N]
  $$
- 单位面积上的内摩擦力，即切应力如下：
- $$
  \tau=\mu\frac{du}{dy}\qquad[N/m^2]
  $$
- 满足牛顿内摩擦定律的流体称为牛顿流体，否则称为非牛顿流体
- $\mu$：流体动力粘滞系数（绝对粘度）$[Pa· s]$
- $$
  \displaystyle[\mu]=\frac{\tau}{[\frac{du}{dy}]}=\frac{[N/m^2]}{[1/s]}=[Pa·s]
  $$
- $\nu$：流体运动粘滞系数（运动粘度）$[m^2/s]$
- $$
  \nu = \frac{\mu}{\rho}
  $$
- 注意：$\nu_{空气}>\nu_{水}$
- 随着温度升高，液体的粘性系数下降；气体的粘性系数上升
- 解释：粘性=分子间吸引力+热运动产生动量交换

粘性作用	分子间吸引力	热运动产生动量交换
温度升高	下降	上升
温度下降	上升	下降

液体：吸引力是主要决定因素，气体：热运动产生动量交换是决定性因素

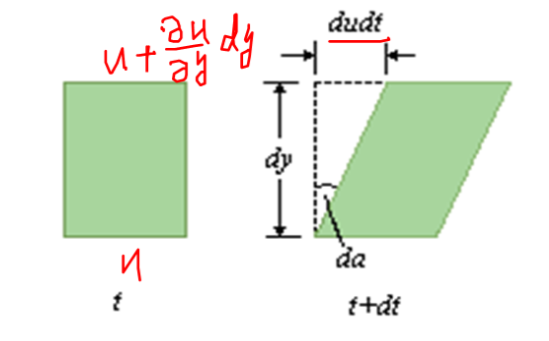
$\displaystyle\frac{du}{dy}$为速度梯度。实际上是流体微团的剪切变形（角）速度，表示流体微团直角减小的速度

$$
底面速度=u \
顶面速度=u+\frac{\partial u}{\partial y}dy \
\frac{d\theta}{dt}=\frac{du}{dy} \
$$

理想流体假设
- 忽略粘性影响的假设：可近似反映粘性作用不大的实际流动，粘性作用不大（相对其他因素而言）
- 忽略粘性即是忽略切应力，切应力
- $$
  \frac{du}{dy}\downarrow\quad,\mu\downarrow\quad\to \tau\downarrow
  $$
- $\mu$是流体的客观属性，所以往往是在速率不大的地方简化为理想流体（原理固体边界壁的边界层流动）
流体的压缩性和膨胀性
- 流体的压缩性是指流体受压、体积缩小、密度增大，除去外力后能恢复原状的性质
- 体积压缩系数$\displaystyle\alpha_p=-\frac{dV/V}{dp}=\frac{d\rho/\rho}{dp}$
- 流体的膨胀性是指流体受热，体积膨胀，密度减小，温度下降后能恢复原状的性质
- 体积膨胀系数$\displaystyle\alpha_\nu=\frac{dV/V}{dT}=-\frac{d\rho/\rho}{dT}$
- 液体一般可不考虑压缩性，作不可压缩流体假设，密度为常数。若考虑水下爆炸、水击问题，必须考虑压缩性
- 空气压缩性很大，但 Ma<0.3 认为是不可压缩的
不可压缩流体假设
- 不可压缩流体假设忽略压缩性和膨胀性，认为流体的密度为常数
- 一般都可看做不可压缩流体，但是水下爆炸，水击，热水采暖必须考虑压缩性、膨胀性
- 气体来说，当气流速度远小于音速，密度变化不大时亦可采用该假设
表面压力（液体的特性，气体没有表面张力？）

液体自由表面上能够承受及其微小的张力，使表面拉紧的特性

水：H=29.8/d(mm)
通常在利用测压管测量时，要求直径不小于 10mm，以减小由于毛细现象造成页面变化形成的测量误差。