流动阻力和能量损失的两种形式
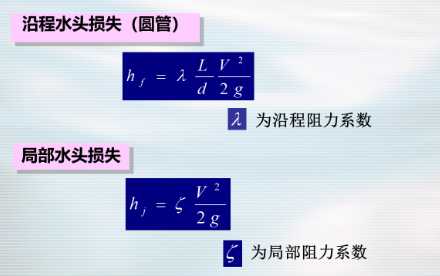
沿程损失与局部损失:
均匀流或渐变流——沿程损失
急变流——局部损失
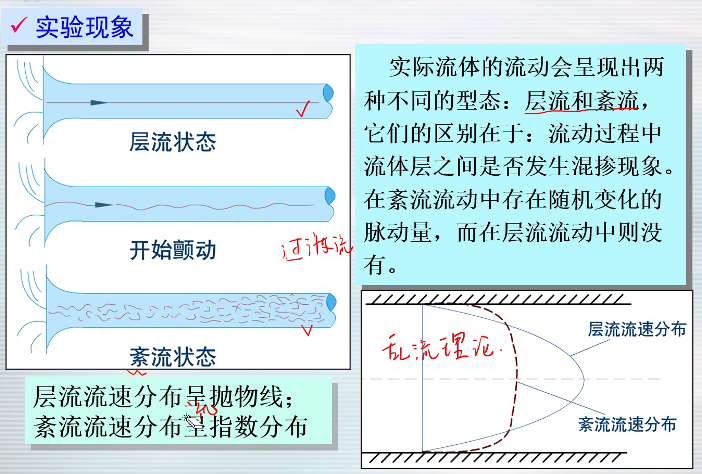
粘性流体的两种流态
- 层流和紊流
- 雷诺实验
- 流态判别——定义一个无量纲数——雷诺数
- 层流和紊流的分界
- 上临界雷诺数:12000-40000
- 下临界雷诺数:2300(便于计算取 2000)
沿程损失和切应力之间的关系
- 在恒定均匀流中取出一段流股
- 然后进行一番操作,就可以进行一些愉快的事情
圆管中的层流运动
这一段全是推导,请看 PPT
紊流流动简介
turbulence——达芬奇
紊流的成因
流动失稳——一门复杂的学科,下面给出粗浅的描述
- 层流流动的稳定性丧失(雷诺数达到临界雷诺数)
- 扰动使某流层产生微小波动
- 流速使波动加剧
- 在横向压差与切应力的综合作用下形成漩涡
- 漩涡受升力而升降
- 引起流体间的掺混
- 造成新的扰动
任意流层上下侧的切应力构成顺时针方向的力矩,有促进漩涡产生的倾向
正反馈——扰动放大
一方面涡体由于惯性作用,有保持其本身运动方向的倾向;另一方面流体有粘性,对于涡体运动有阻力,约束涡体运动。只有当惯性力超过粘滞力,涡体才能脱离原流层掺入新流层,从而变为紊流。
紊流运动的时均化
掺混:
- 流体质点在流动过程中不断相互掺混
运动要素中的脉动:
- 流体中涡体不断的产生、发展、衰减和消失,使固定空间点上的各种运动要素,如速度、压强、浓度等都随时间不断波动,称为脉动。
- 统计平均的方法有很多:对时间(希望)、空间、集合(系统平均)都可以取平均,在“各态历经”假设成立的前提下,一般采用时间平均法时间平均法: 将紊流的流动看作是时间平均流动和脉动流动的叠加
- 注意其中的 T 需要足够大,这样才可以取平均
- 恒定紊流——时均流动中时均流速不变
紊流的基本方程
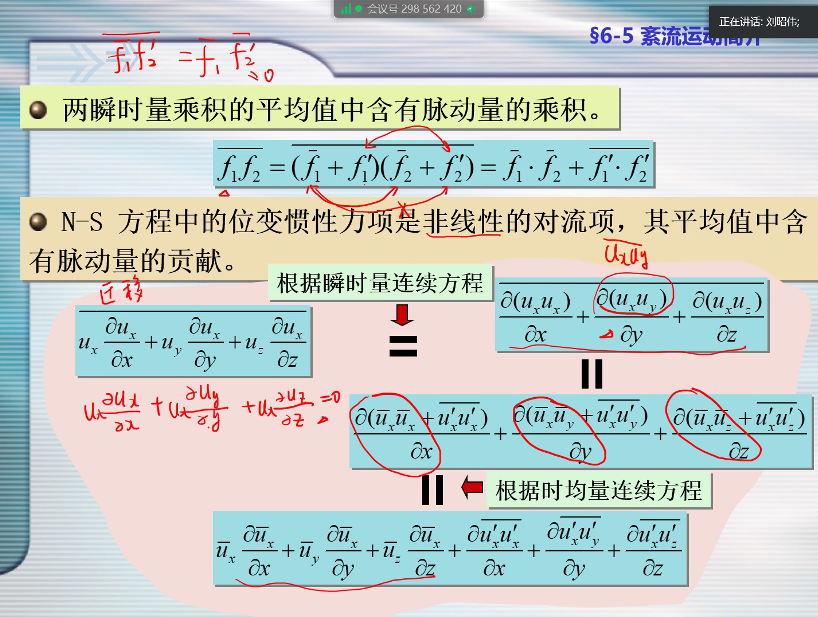
紊流的基本方程指的是时均流场所满足的方程,紊流流动的瞬时量仍满足连续方程和 N-S 方程。
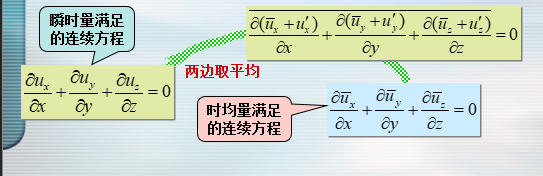
通过对瞬时量所满足的连续方程和 N-S 方程两边取平均的方法可以得到紊流时均流动的连续方程和运动方程。
因为连续方程的各项都是线性项,取平均值后脉动量不出现。
紊流的半经验理论
混合长度理论是最基本的一种寻求雷诺应力与平均流速关系的半经验理论。
混合长度理论假设微团垂向移动 l1后,进入并与相邻流层混合,类比于分子运动的自由程。
紊流中壁面附近切应力和流速的分布
把壁面附近紊流时均流动看作由主流带动的无压均匀流
紊流沿程损失的分析与计算
尼古拉兹实验
一些公式
- 绝大部分公式无法推导——这些公式来源于莫迪图
谢才公式
$$
V=C\sqrt{RJ}
$$
谢才系数 C 的确定,可以使用曼宁公式和巴氏公式











