运动流体的应力状态
动压强与静压强
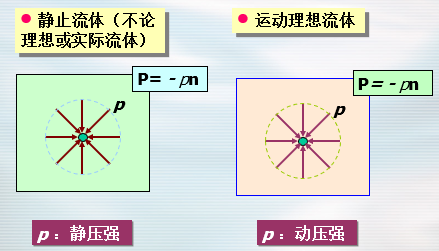
- 质量力比表面力搞一个小量——先趋于零
- 因而可以证明$p_n=p_y$
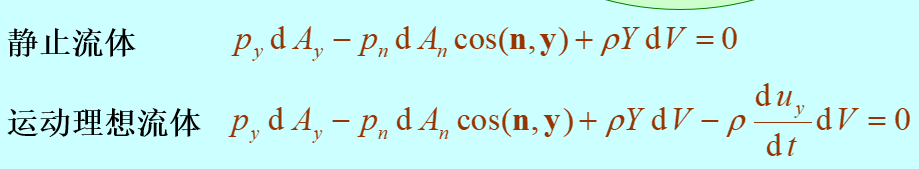
- 角标含义与材料力学相同,前一个表示作用面方向;后一个表示应力分量之投影方向。
- 作用面的法向方向!
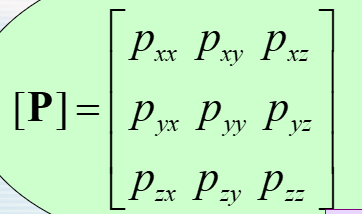
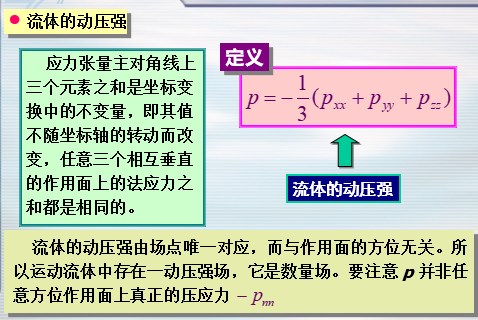
- 应力张量:九个量组成的二阶张量
- 主对角线上的三个元素是法应力分量,其它是切应力分量。
- 可以证明这个张量是对称的,只有六个独立的分量。
- 有了这个张量,就可以描述任意方位作用面上的应力——法向量点乘张量。
- 运动流体的应力状态可由应力张量来描述。
广义牛顿内摩擦定律
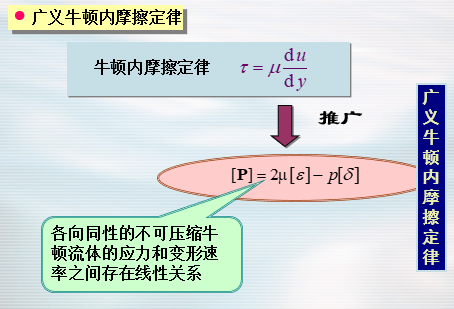
流体运动微分方程
- 按照欧拉观点表述动量守恒定律:单位时间控制体内动量的增加必等于单位时间净流入控制体的动量加上控制体内流体所受合力。
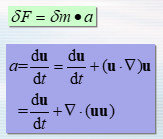

- 与连续方程构成了描述理想流体运动的方程组
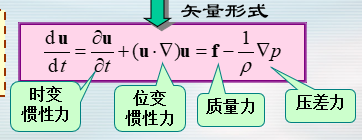
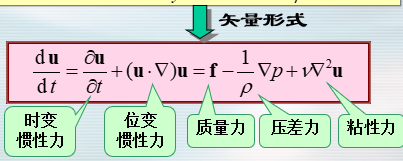
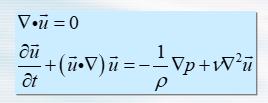
- 流体动力学定解问题=流体运动基本方程+初始条件/边界条件
- 对空间求导——称为边界条件
- 边界条件是指运动方程的解在流场的边界上必须满足的运动学和动力学条件。常见的边界条件有:固壁条件和液体的自由表面条件。
- 与 t 相关的条件——初始条件
- 初始条件是对非恒定流动指定初始时刻流场的速度和压强分布。
边界条件:理想流体的固壁条件称为可滑移条件,即流体不能穿越固壁,但可有切向相对运动,所以
$$
u_n=U_n
$$
- 实际(粘性)流体的固壁条件称为不可滑移条件,即附着在固壁上的流体质点与固壁不能有相对运动,所以
$$
u=U
$$

液体的自由表面动力学条件为自由表面上压强为常数(大气压)。
应用
流动 1:匀速平板带动的流体流动

- 在某种情况下——我们可以得到牛顿内摩擦定律得到的流动分布
流动 2:圆管层流
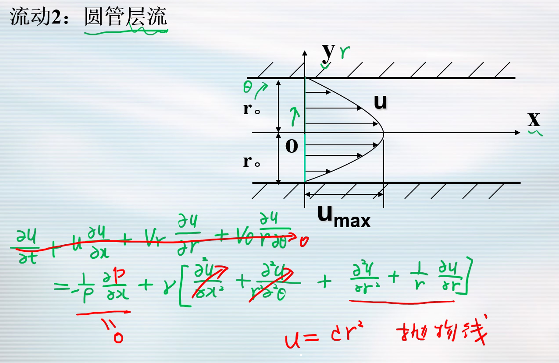
理想流体恒定元流的能量方程
- 先讲流线
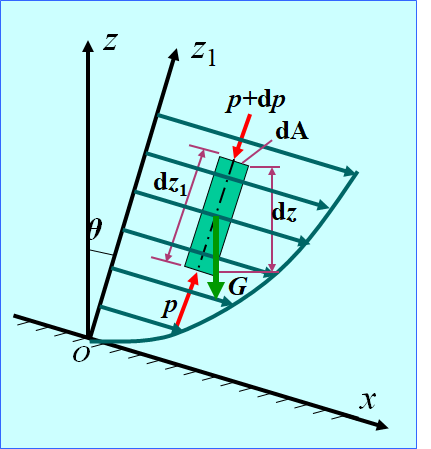
理想流体的运动微分方程的积分
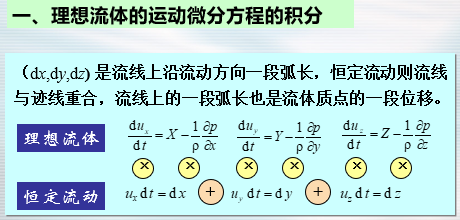

- 重力和科氏力——重力:有势;科氏力没有势

- 在理想流体的恒定流动中,同一流线上各点的
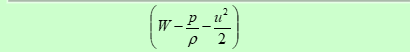
- 值是一个常数。其中 W 是质量力势函数,r 是不可压缩流体的密度。从推导过程看,积分是在流线上进行的,所以不同的流线可以有各自的积分常数,将它记作 C
1,称为流线常数。当流动为无旋流动时,流线常数均相等。 - 伯努利积分是在一定条件下对理想流体运动方程(欧拉方程)沿流线的积分。
- 注意条件:
- 理想流体;
- 流体不可压缩,密度为常数;
- 流动恒定;
- 质量力是有势的;
- 沿流线积分。
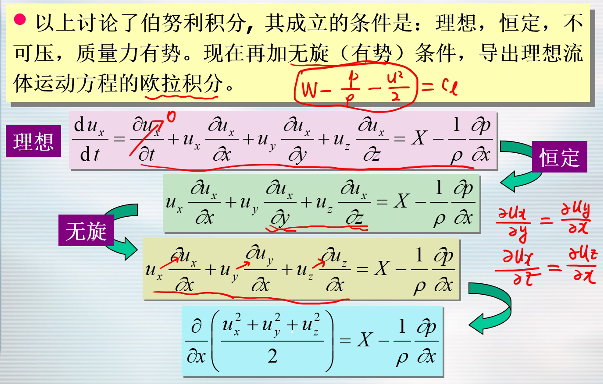
- 经过一系列小学二年级就会的运算(Orz)

- 表面上看,伯努利积分和欧拉积分很相似,但两者的适用条件和使用范围是截然不同的。
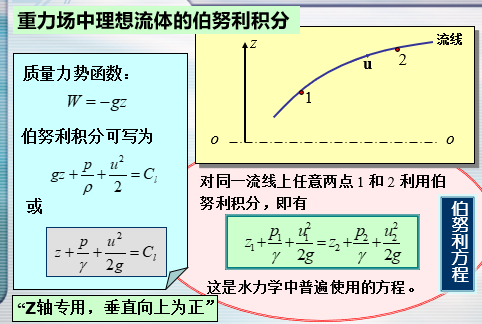
- 伯努利方程表示能量的平衡关系。
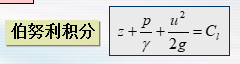
- z——单位重量流体所具有的位置势能(简称单位位置势能)
- $\displaystyle\frac{p}{\gamma}$——单位重量流体所具有的压强势能(简称单位压强势能)
- $z+\displaystyle\frac{p}{\gamma}$——单位重量流体所具有的总势能(简称单位总势能)
- $\displaystyle\frac{u^2}{2g}$——单位重量流体所具有的动能(简称单位动能)
- $z+\displaystyle\frac{p}{\gamma}+\frac{u^2}{2g}$——单位重量流体所具有的动能(简称单位动能)
欧拉观点:在理想流体的恒定流动中,位于同一条流线上任意两个流体质点的单位总机械能相等。
拉格朗日观点:在理想流体的恒定流动中,同一流体质点的单位总机械能保持不变。
- 总机械能不变,并不是各部分能量都保持不变。三种形式的能量可以各有消长,相互转换,但总量不会增减。
- 伯努利方程是能量守恒原理在流体力学中的具体体现,故被称之为能量方程。
- 伯努利方程在流线上成立,也可认为在元流上成立,所以伯努利方程也就是理想流体恒定
元流 的能量方程。 - 伯努利方程可理解为:元流的任意两个过水断面的单位总机械能相等。由于是恒定流,通过元流各过水断面的质量流量相同,所以在单位时间里通过各过水断面的总机械能(即能量流量)也相等。
几何意义
- 伯努利积分各项都具有长度量纲,几何上可用某个高度来表示,常称作水头。
- z——位置水头
- $\displaystyle\frac{p}{\gamma}$——压强水头
- $z+\displaystyle\frac{p}{\gamma}$——测压管水头
- $\displaystyle\frac{u^2}{2g}$——速度水头
- $z+\displaystyle\frac{p}{\gamma}+\frac{u^2}{2g}$——总水头
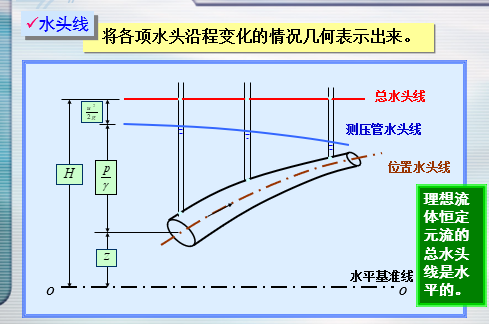
应用举例
- 测流速——毕托管测速仪
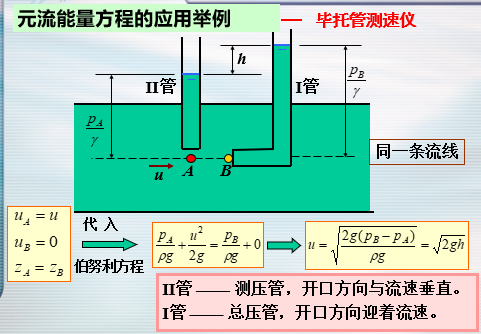
- 实际上,会有一个修正系数
- 不同的毕托管不同
恒定总流的能量方程
理想流体恒定总流的能量方程
- 在总流中,选取两个渐变流断面 1、2。因为总流可以看作无数个元流的总和,因此,总流能量方程可以由元流能量方程在两断面范围内积分来得到。
- 渐变流当作均匀流来考虑
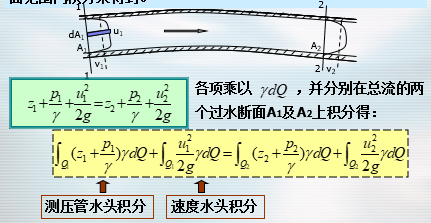
- 恒定均匀流特性:
- 1.均匀流的过水断面为平面,且过水断面的形状和尺寸沿程不变。
- 2.均匀流中,同一流线上不同点的流速应相等,从而各过水断面上的流速分布相同,断面平均流速相等。
实际流体恒定总流的能量方程
断面 A1 是上游断面,断面 A2 是下游断面,hw1-2 为总流在断面 A1 和 A2 之间平均每单位重量流体所损耗的机械能,称为水头损失。水头损失分为沿程水头损失和局部水头损失,如何确定,将在后面叙述。
- 流动必须是恒定流,并且流体是不可压缩的。
- (2)作用于流体上的质量力只有重力。
- (3)所取的上下游两个断面应在渐变流段中,以符合断面上测压管水头等于常数这一条件。但在两个断面之间流动可以不是渐变流。断面应选在已知条件较多的位置。在渐变流断面上取任何一点的测压管水头值都可作为整个断面的平均值,为简便通常取管道中心点或渠道水面点。
恒定总流能量方程的几何表示——水头线
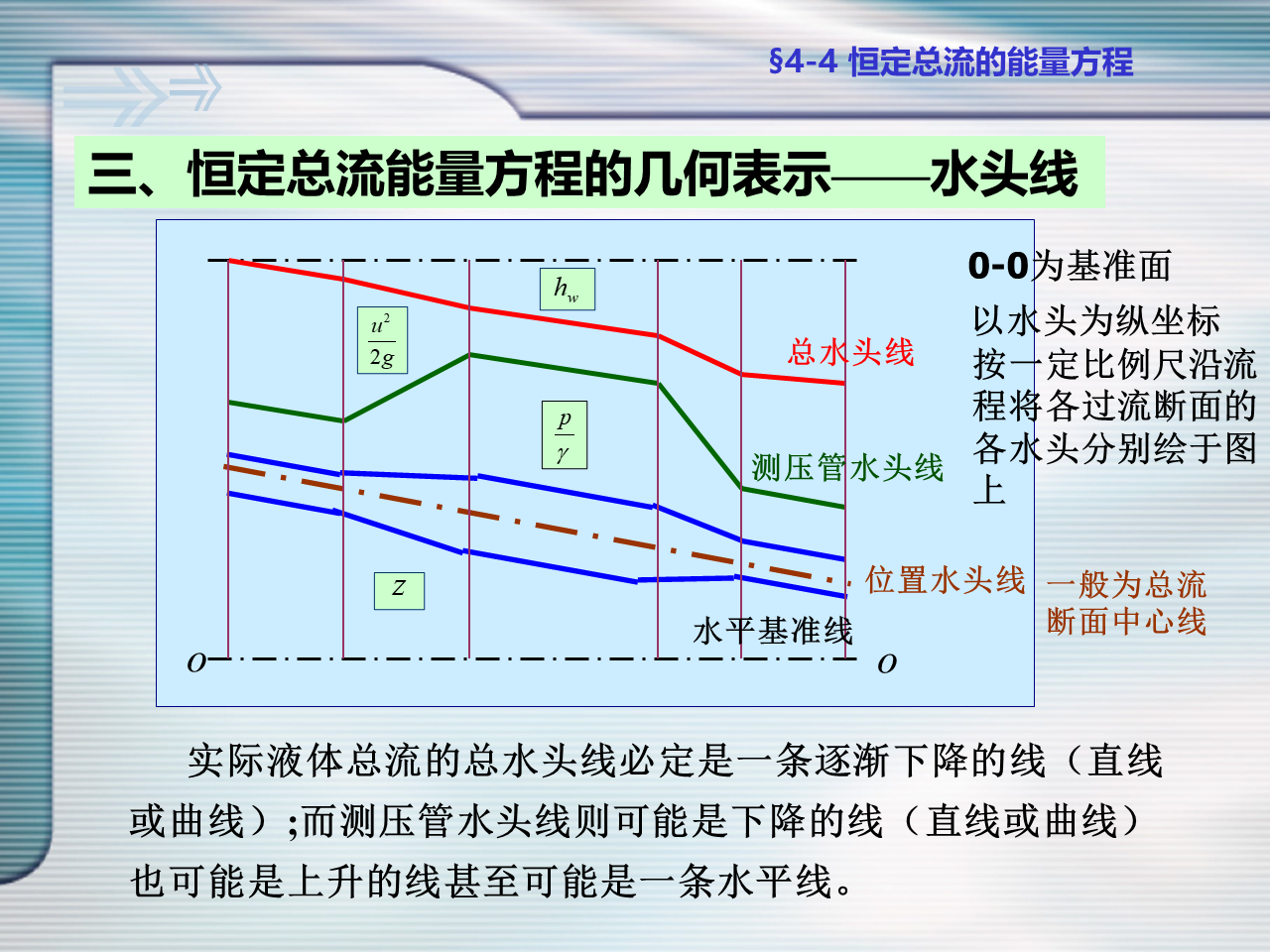
- 水力坡度和水面坡度看起来很像
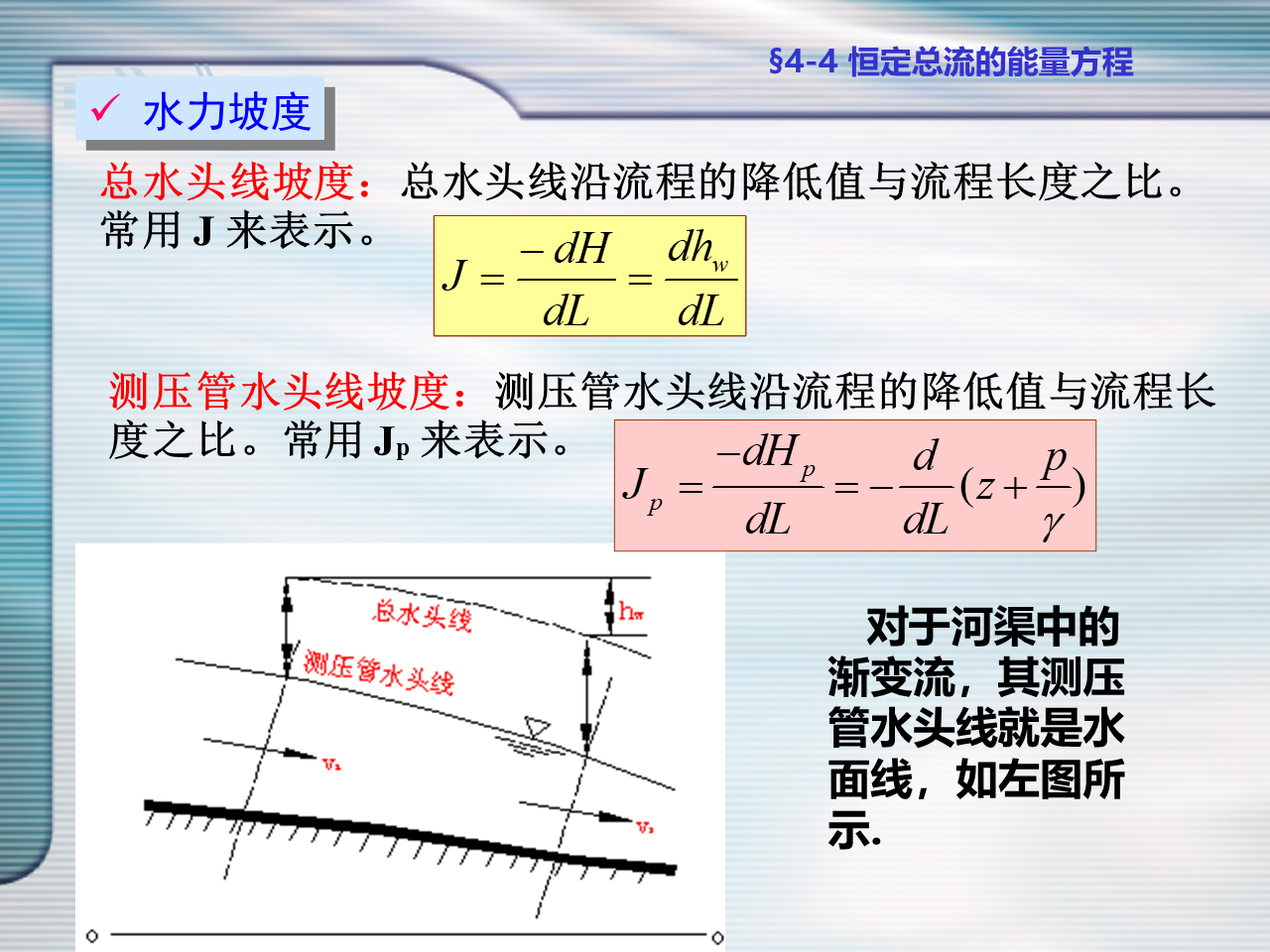
应用
- 文透里管
文透里管测流量
文透里管是一种常用的量测管道流量的装置,它包括收缩段、喉道和扩散段三部分,安装在需要测定流量的管道上。在收缩段进口断面 1-1 和喉道断面 2-2 上接测压管,通过量测两个断面的测压管水头差,就可计算管道的理论流量 Q ,再经修正得到实际流量。
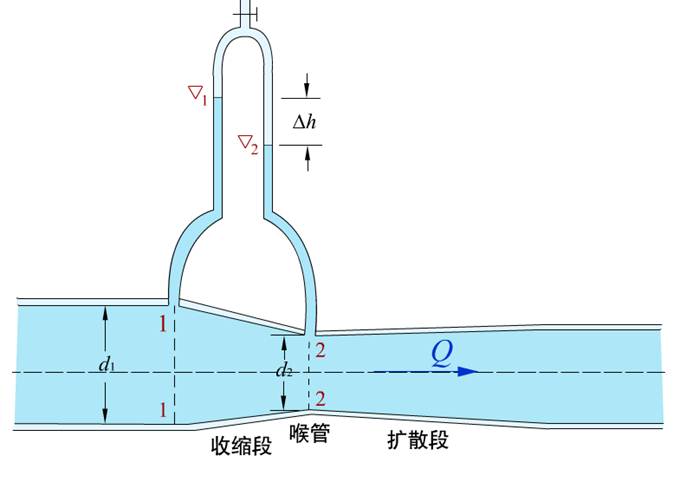
$Q_实=\mu K \sqrt{\Delta h}$
文透里管能否斜置?
可以,并且没有变化,可以不用修正,直接使用$\Delta h$即可
上下游倒置?
需要修正!修正系数究竟是多少需要考虑
有能量输入或输出的能量方程

水泵管路系统
水轮机系统
水轮机功率:
汇流、分流的能量方程
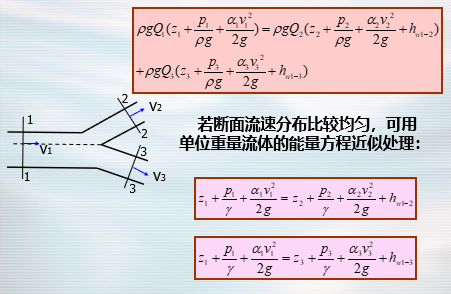
注意事项
- 同一基准面
- 以方便计算为宜
- 注意绝对压强与相对压强
- 注意动能修正系数
恒定总流的动量方程
动量守恒原理表述如下:单位时间控制体内动量的增加等于单位时间净流入控制体的动量加上控制体内流体所受合力。
恒定流动:控制体内动量不会改变、没有流体穿过总流管侧壁流入或流出,动量只能通过两个过流断面进出控制体。










