一道可能不太简单的解三角形题
题目
已知$a,b,c$分别为$\Delta ABC$的内角$A,B,C$对应的边,$BC$边上的高为$\displaystyle \frac{a}{2}$,求$\displaystyle \frac{c}{b}$最大值.
分析
本题有多种解法,部分解法较难想到
在$\Delta ABC$中,由余弦定理,有
$$
\begin{equation}\label{equationa}
\begin{aligned}
b^2+c^2&=a^2+2bc\ cosA \newline
\Rightarrow 1+\left(\frac{c}{b}\right)^2&=\left(\frac{a}{b}\right)^2 + 2\frac{c}{b}cosA
\end{aligned}
\end{equation}
$$
又有
$$
\begin{equation}\label{equationb}
\begin{aligned}
S_{\Delta ABC} = \frac{1}{2}bc\ sinA&=\frac{1}{2}a\cdot\frac{a}{2} \newline
\Rightarrow \left(\frac{a}{b}\right)^2&=2\frac{c}{b}sinA
\end{aligned}
\end{equation}
$$
由公式$(\ref{equationa})$、$(\ref{equationb})$,得
$$
\begin{equation}
\begin{aligned}
1+\left(\frac{c}{b}\right)^2&=2\frac{c}{b}sinA + 2\frac{c}{b}cosA
\end{aligned}
\end{equation}
$$
令$\displaystyle \frac{c}{b} = t$,得
$$
\begin{equation}
\begin{aligned}
1+t^2&=2t(sinA+cosA)=2\sqrt{2}tsin\left(A+\frac{\pi}{4}\right) \newline
\Rightarrow t+\frac{1}{t}&=2\sqrt{2}sin\left(A+\frac{\pi}{4}\right)\in [\ 2,2\sqrt{2}\ ] \newline
\Rightarrow t_{max} &= \sqrt{2} + 1
\end{aligned}
\end{equation}
$$
故$\displaystyle \frac{c}{b}$最大值为$\sqrt{2} + 1$.
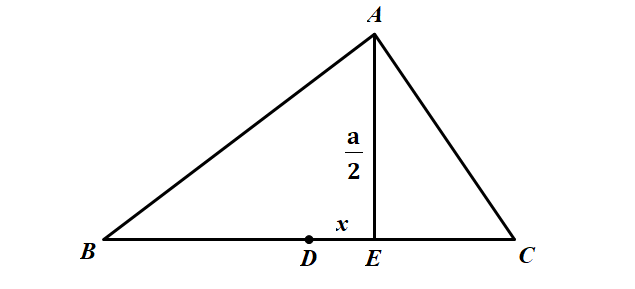
如图,利用勾股定理有
$$
\begin{aligned}
AB&=\sqrt{\left(\frac{a}{2}+x\right)^2+\left(\frac{a}{2}\right)^2} \newline
AC&=\sqrt{\left(\frac{a}{2}-x\right)^2+\left(\frac{a}{2}\right)^2} \newline
\Rightarrow\quad \frac{c}{b}&=\frac{\sqrt{\left(\frac{a}{2}+x\right)^2+\left(\frac{a}{2}\right)^2}}{\sqrt{\left(\frac{a}{2}-x\right)^2+\left(\frac{a}{2}\right)^2}} \newline
&=\sqrt{\frac{\frac{a^2}{2}+ax+x^2}{\frac{a^2}{2}-ax+x^2}} \newline
&=\sqrt{1+\frac{2ax}{\frac{a^2}{2}-ax+x^2}} \newline
&=\sqrt{1+\frac{2}{\frac{a}{2x}+\frac{x}{a}-1}}\newline
&\leq\sqrt{1+\frac{2}{2\sqrt{\frac{a}{2x}\cdot\frac{x}{a}}-1}}\newline
&=\sqrt{1+\frac{2}{\sqrt{2}-1}}\newline
&=\sqrt{2}+1
\end{aligned}
$$
当且仅当$\displaystyle\frac{a}{2x}=\frac{x}{a}$时取得最大值,即
当$\displaystyle x=\frac{\sqrt{2}a}{2}$时,$\displaystyle \frac{c}{b}$最大,为$\sqrt{2} + 1$.
根据阿氏圆,及数形结合方法,可知,阿氏圆半径需不小于$\displaystyle \frac{a}{2}$,由半径公式,即
$$
\begin{aligned}
\left|\frac{\mu}{\mu^2-1}\right|\cdot a &\geq \frac{a}{2} \ , \quad \mu > 0 \newline
\mu_{max} &=\sqrt{2}+1
\end{aligned}
$$
又由于$\displaystyle \frac{c}{b}=\mu$,故
$\displaystyle \frac{c}{b}$最大值为$\sqrt{2} + 1$.
答案
本题答案为$\sqrt{2} + 1$










